Оценка достоверности результатов исследования
Эталон решения
1.Доля городского в общей численности населения
= численность городского населения х100
среднегодовая численность населения
= 92000 х100= 69,7%
2. Доля детского в общей численности населения
=численность детского населения х100
среднегодовая численность населения
= 21380 x100 = 16,2%
3. Доля лиц в возрасте старше 50 лет
в общей численности населения
=численность лиц в возрасте старше 50 лет х100
среднегодовая численность населения
= 42000 х100 = 31,82%
4. Доля мужчин в общей численности населения
= численность мужчин х100
среднегодовая численность населения
= 62000 x100 = 47%
Относительные величины,
показатели динамического ряда,
Основные вопросы темы:
1. Абсолютные цифры и статистические показатели
2. Относительные величины
3. Показатели динамического ряда.
4. Достоверность статистических показателей.
Для статистического анализа, т.е. сравнения, сопоставления чаще всего используются:
1) абсолютные цифры
2) средние величины
3) относительные величины
4) показатели динамического ряда
Абсолютные цифры чаще всего используют в двух случаях:
1) когда число всесторонне характеризует явление
Например: численность населения области, врачебного участка, количество коек в ЛПУ…
2) статистические показатели не рассчитывают, если n < 30
Например: пролечено 10 пациентов с мезентеральным тромбозом, 5 умерло. Нельзя сказать, что летальность 50 %.
Чаще всего в статистическом анализе используются относительные величины.
Наиболее часто употребляются:
1) интенсивные показатели
2) экстенсивные показатели
3) показатели соотношения
4) показатели наглядности
Экстенсивный показатель – это показатель структуры явления, т.е. показатель распределения.
Например, в здравоохранении часто рассчитывают
1. структуру смертности
2. структуру заболеваемости
3. распределение обслуживаемого населения по группам здоровья
4. структуру обслуживаемого населения по полу, возрасту…
Формула расчета экстенсивного показателя:
| Экстенсивный показатель | = | Абсолютный размер части явления | Х 100 % |
| Абсолютный размер явления в целом |
Основные правила
пользования экстенсивным показателем
1) нельзя применять для изучения динамики явления во времени
2) нельзя пользоваться для сравнения степени распространения изучаемого явления в различных совокупностях
3) можно пользоваться для сравнения показателей в одно время в одном месте (правило единого места и времени)
Графически представляют экстенсивный показатель чаще в виде:
1. секторной диаграммы
2. внутристолбиковой диаграммы
3. объемной или фигурной диаграммы с выделением сектора и
части
Интенсивный показатель – это показатель частоты, распространенности явления в среде, порождающей данное явление.
Средой в нашем случае чаще являются население.
Как интенсивный показатель в здравоохранении считают:
1. показатели рождаемости
2. показатели смертности
3. показатели заболеваемости
4. показатели инвалидности…
Формула расчета интенсивного показателя
| Интенсивный показатель | = | Абсолютный размер явления Х 1000 |
| Абсолютный размер среды, продуцирующей данное явление |
Правила использования интенсивного показателя:
Интенсивный показатель можно сравнить как в динамике, так и в разных совокупностях, но необходимо помнить о качественном составе сравниваемых явлений.
Графически интенсивный показатель представляют чаще в виде:
1. столбиковой диаграммы
2. картограммы
3. картодиаграммы
Показатель соотношения – это показатель распространения явления в среде с ним не связанной, не продуцирующей данное явление.
Как показатель соотношения в здравоохранении считают обеспеченность населения
1. врачами
2. средним медицинским персоналом
3. больничными койками
Формула расчета показателя соотношения:
| Показатель соотношения | = | Абсолютный размер явления Х 10 000 (100 000) |
| Абсолютный размер среды, не продуцирующей данное явление |
Показатель соотношения можно использовать для сравнения чего-либо в динамике и для распространенности явления в разных совокупностях (обеспеченность койками в разные годы или в разных регионах).
Графически показатель соотношения может быть представлен в виде:
1. столбиковой диаграммы
2. фигурной диаграммы
3. объемной диаграммы
4. картограммы
5. картодиаграммы
Показатель наглядности характеризует динамику явления во времени. Исходная величина при этом принимается за 100 % или за единицу.
Формула расчета показателя наглядности:
| Показатель наглядности | = | Явление | Х 100 % |
| Такое же явление, принятое за соизмеритель или 100 % |
Графически показатель наглядности может быть представлен в виде:
1. линейной диаграммы
2. ряда столбиковых, объемных или фигурных диаграмм
Показатели динамического ряда применяются для анализа динамики явления во времени.
Анализ динамических рядов можно проводить по комплексу показателей:
1. показатель наглядности
2. коэффициент роста (убыли)
3. тем прироста (убыли)
4. абсолютный прирост
5. значение 1 % прироста
Коэффициент роста – это отношение каждого последующего члена ряда к предыдущему, выраженное в процентах:
| Коэффициент роста | = | Последующий уровень | Х 100 % |
| Предыдущий уровень |
Темп прироста – это отношение разности сравниваемых величин к исходному уровню, выраженное в процентах:
| Темп прироста | = | Последующий уровень - предыдущий уровень | Х 100 % |
| Предыдущий уровень |
Достоверность статистических показателей - это степень их соответствия отображаемой действительности.
Оценка достоверности предусматривает определение:
1. ошибок репрезентативности (m)
2. доверительных границ М и Р
3. достоверности разности М и Р
Определение достоверности обусловлено тем, что исследования проводят чаще на выборочных совокупностях, а по их результатам характеризуют генеральную совокупность.
По величине ошибки репрезентативности определяют, насколько результаты, полученные при выборочном исследовании, отличаются от результатов, которые могли бы быть получены при сплошном исследовании.
Ошибка М определяется по формуле:
| mM | = | s |
| √n |
где s - среднее квадратическое отклонение
- среднее квадратическое отклонение
n - число наблюдений
Т.е. mM зависит от:
1. числа наблюдений
2. разнообразия признака в исследуемой совокупности
 |
| p x q |
| n |
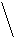
 mp =
mp =
где: р – относительная величина (само явление)
q – часть среды, где явление не распространено
q = 100 – р (если р в % )
q = 1000 – р (если р в ‰)
n – число наблюдений
Если n < 30 то в данной формуле в знаменателе (n–1)
Доверительность границы – это границы М или Р, выход за пределы которых имеет незначительную вероятность.
Они определяются по формулам:
Мген = Мвыб ± tm
Рген = Рвыб ± tm
где t – критерий точности
Величина t зависит от вероятности безошибочного прогноза (Р )
если Р = 95 %, t =2
если Р =99 %, t =3
В большинстве работ Р принимают за 95 % т.е. t =2.
Определение достоверности разности средних или относительных величин.
Очень часто бывает необходимо сравнить М и Р, полученные на двух выборочных совокупностях.
Для этого используют следующие формулы:
| t | = | M1 – M2 |
 
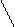  m1² + m2² m1² + m2²
|
| t | = | P1 – P2 |
 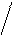 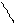  m1² + m2²
m1² + m2²
|
где : М1, M2, Р1, Р2 – это средние и относительные величины, полученные при выборочных исследованиях.
m1 и m2 - их средние ошибки
t - критерий достоверности
Разность достоверна при t ≥ 2 (т.е. две величины отличаются достоверно друг от друга).
При t < 2 считают доказанным, что между сравниваемыми совокупностями не обнаружено достоверных различий по изучаемому признаку.
Например:
1. уровни летальности в 2 ЛПУ
2. заболеваемость в 2 регионах
3. смертность в 2 странах от чего-либо…