Равномерное распределение энергии по степеням свободы молекул

Внутренняя энергия системы - энергия, зависящая
только от её внутреннего состояния; она складывается из
кинетической энергии хаотического движения атомов или
молекул, потенциальной энергии межмолекулярных взаимо-
действий и энергии внутриатомных движений и взаимодей-
ствий. Поскольку в модели идеального газа потенциаль-
ная энергия межмолекулярных взаимодействий полагается равной нулю, то внутренняя энергия идеального газа определя- ется кинетической энергией теплового движения его молекул. В свою очередь энергия теплового движения молекул зависит от числа степеней свободы.

Числом степеней свободы тела называется число независимых координат, полностью определяющих положение тела в пространстве. Если одноатомную молекулу рассмат- ривать как материальную точку, то для описания её положения в пространстве достаточно трёх независимых координат. Следовательно, одноатомная молекула имеет три степени свободы. Двухатомная молекула с жёсткой связью между атомами имеет пять степеней свободы. Три из них определяют поступательное движение молекулы, две - вращательное. Если в молекуле три (и более) атома, связанных жёсткой связью, то число степеней свободы равно 6. Во многих случаях необходи- мо принимать во внимание возможность относительных смещений атомов в молекуле, т.е. вводить в рассмотрение колебательные степени свободы молекул.

Согласно закону Больцмана о равномерном распределе- нии энергии по степеням свободы молекул все степени свободы равноправны и вносят одинаковый вклад в ее сред- нюю энергию. Учитывая, что средняя энергия поступатель- ного движения одноатомной молекулы по формуле (2.7), равна

,

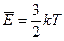получим кинетическую энергию, приходящуюся на одну степень свободы

. (3.1)

Если молекула имеет ί степеней свободы, то ее средняя кинетическая энергия

, (3.2)

где .

Колебательная степень обладает вдвое большей энергией поскольку на нее приходится не только кинетическая энергия, но и потенциальная, причем средние значения кинетической и потенциальной энергий одинаковы.

С учетом (3.2), внутренняя энергия одного моля идеаль- ного газа равна

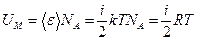, (3.3)

а произвольной массы газа

. (3.4)

Таким образом, внутренняя энергия идеального газа зависит от числа степеней свободы молекул и абсолютной температуры. Внутренняя энергия – однозначная функция состояния системы, она не зависит от пути перехода в данное состояние.

Изменение внутренней энергии газа связано с изменением температуры

. (3.5)