Следствия из преобразований Лоренца

 

Постулаты специальной теории относительности требовали новых правил перехода от одной инерциальной системы отсчета к другой. Такие правила, а именно, новые преобразования координат и времени были получены Лоренцем.

Предположим, что происходит какое-то событие. В системе оно характеризуется значением координат и времени (x,y,z,t). В системе (рис.1.17), движущейся относительно системы с постоянной скоростью , направленной вдоль совпадающих осей и , - значениями координат и времени ( ). Формулы, связывающие штрихованные и нештрихованные значения координат и времени, имеют следующий вид

, (1.92)

. (1.93)

Здесь с – скорость света, .

Из данных формул видно, что при преобразова- ния Лоренца переходят в преобразования Галилея (1.88). Это означает, что различие в течение времени в разных системах отсчета обусловлено существованием предельной скорости распространения взаимодействий.

При скоростях много меньших скорости света ( ) преобразования Лоренца не отличаются от преобразований Галилея. Следовательно, преобразования Галилея не теряют своего значения, и могут быть использованы при малых по сравнению со скоростью света скоростях.

Наконец, при выражения для координат и времени в формулах (1.92) и (1.93) становятся мнимыми, свидетель- ствуя о том, что движение со скоростями большими скорости света в вакууме невозможно. Невозможна и система отсчета, движущаяся со скоростью , поскольку при знаменатели формул (1.92) и (1.93) обращаются в нуль.

 

Из преобразований Лоренца вытекает ряд необычных с точки зрения ньютоновской механики следствий.

Сокращение длины. Рассмотрим стержень, расположен- ный вдоль оси и покоящийся относительно системы отсчета (рис.1.19). Длина его в этой системе равна

,

где 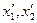- не изменяющиеся со временем координаты концов стержня. Относительно системы стержень движется вместе с системой со скоростью . Для определения его длины в этой системе нужно отметить координаты концов стержня в один и тот же момент времени . Разность этих координат даст длину стержня, измеренную в системе . Для нахождения соотношения между и , воспользуемся преобразованиями Лоренца

,

откуда получаем

. (1.94)

Таким образом, длина стержня , измеренная в системе, относительно которой он движется, оказывается меньше «собственной» длины , измеренной в системе, относи- тельно которой он покоится. Поперечные размеры стержня в обеих системах одинаковы. Итак, для неподвижного наблюдателя размеры движущихся тел в направлении их движения сокращаются, и тем больше, чем больше скорость движения.

Замедление времени. Пусть в системе в одной и той же точке с координатой происходит какое-то событие, длящееся время . Относительно системы точка, в которой происходит это событие, перемещается. Согласно формулам (1.93), началу и концу события в системе соответствуют моменты времени

,

отсюда получаем

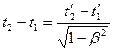или . (1.95)

В этой формуле - время, отсчитанной по часам, движущимся вместе с телом. Это время называется собственным временем и обычно обозначается буквой . Время измерено по часам системы, относительно которой тело движется со скоростью .

Рассматривая прошедшее событие из системы , можно определить как его длительность, измеренную по неподвижным часам, а - как длительность, измерен- ную по часам, движущимся вместе с телом. Представляя формулу (1.95) в виде

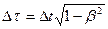, (1.96)

можно сказать, что движущиеся часы идут медленнее, чем покоящиеся . Эта зависимость особенно сильно проявляется при скоростях, сравнимых со скоростью света.

Замедление времени является следствием постоянства скорости света во всех системах отсчета. Эффект замедления времени в настоящее время с высокой точностью подтверждается экспериментально.

Относительность одновременности разнесенных в пространстве событий. Пусть в системе в точках с координатами x₁ и x₂ происходят одновременно два события в момент времени . В системе этим событиям будут соответствовать моменты времени

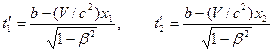. (1.97)

Из полученных формул видно, что пространственно разобщенные и одновременные в системе события, не будут одновременными в системе . При этом разность будет различна по величине и может отличаться по знаку в различных системах отсчета.

Закон сложения скоростей. Ввиду того, что согласно преобразованиям Лоренца, изменяются не только координаты, но и время, меняется и закон сложения скоростей.

Если в системе тело движется со скоростью , имею- щей составляющие по осям координат , то в системе для составляющих скорости тела, получаем

. (1.98)

В частности, положив в (1.98) , получим

. (1.99)

Этот результат не является удивительным, поскольку в основе преобразования Лоренца лежит инвариантность скорости света.