Динамические параметры и характеристики

 

В реальных системах автоматики сигналы от элементов, как пра­вило, бывают непостоянными. В большинстве случаев они меня­ются во времени. Для элементов, составляющих системы автома­тики, основным режимом работы является режим, при котором входная и выходная величины не остаются постоянными. Такой режим называется динамическим.

Для оценки работы элемента в динамическом режиме исполь­зуются динамические характеристики и параметры.

Процесс перехода элемента из одного установившегося состоя­ния в другое называют переходным процессом. Так как во время переходного процесса Y изменяется, то переходный процесс, следовательно, является частным случаем динамического ре­жима.

Переходный процесс характеризуется переходной характери­стикой. Под переходной характеристикой понимают зависимость выходной величины от времени Y = f(t) при скачкообразном изменении входной величины. Реакция большинства элементов на скачкообразный входной сигнал (рис. 5.3,а), т. е. их переходная характеристика (рис. 5.3, б), представляет собой нарастаю­щую экспоненту.

Время от начала экспонен­циального изменения выходной величины до момента, когда она достигает 63% (²/з) уста­новившегося значения выход­ной величины, называется по­стоянной времени элемента τ.

Чем меньше τ, тем круче бу­дет переходная характеристи­ка, тем меньше длительность переходного процесса и тем меньше инерционность элемен­та. Динамические свойства эле­мента принято оценивать по его реакции на скачкообразное изменение входного сигнала. При этом переходный процесс, назы­ваемый переходной характеристикой, определяется только свойст­вами элемента. До подачи скачкообразного сигнала на вход эле­мент находится в одном установившемся состоянии (режиме), пос­ле подачи скачка и окончания* изменений выходной величины эле­мент будет находиться в другом установившемся состоянии. Таким образом, переходная характеристика позволяет выявить и оценить инерционность элемента.

Разные по функциональному назначению элементы имеют не­одинаковые динамические свойства, обусловленные разной инер­ционностью элементов, которая проявляется в том, что изменение выходной величины не повторяет мгновенно изменений входной величины, а происходит с некоторым запаздыванием во времени. Например, при скачкообразном изменении входной величины X за счет инерционности элемента его выходная величина Y достиг­нет нового установившегося значения не сразу, а только после окончания переходного процесса.

Кривая зависимости Y=f(t)при скачкообразном изменении входного сигнала является графической интерпретацией решения дифференциального уравнения элемента, которым описывается поведение элемента при переходном процессе, где входные и вы­ходные сигналы являются функциями времени.

Различные элементы автоматики имеют различные графики пе­реходных процессов (рис. 5.4), так как поведение элементов при воздействии на них скачкообразных входных сигналов описывает­ся различными дифференциальными уравнениями.

На рис. 5.4, а показан переходный процесс без запаздывания, на рис. 5.4, б — переходный процесс элементов, обладающих инер­цией. Степень инерционности подобных элементов оценивается по­стоянной времени т. Это время определяется расстоянием по оси абсцисс от начала координат

 

 

 

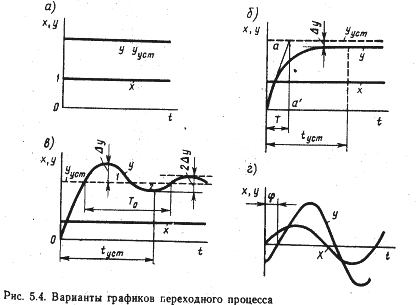
до точки пересечения а касательной к кривой переходного процесса в начале координат с установив­шимся значением выходного сигнала Y_уст. На рис. 5.4, в показан колебательно-затухающий переходный процесс, цри котором вы­ходная величина колеблется около ее установившегося значения Yуст с постоянной частотой f_о=1/τ_о, где τ_о —период колебаний снепрерывно убывающей амплитудой. Время t_уст в течение которого выходной сигнал достигает значения, отличающегося на ΔY от установившегося значения выходной величины Y, называется длительностью переходного процесса. Переходный процесс, показанный на рис. 5.4, в, называется периодическим в отличие от апериодического переходного процесса, показанного на рис. 5.4, б. Выходной сигнал, показанный на рис. 5.4, г, изменяется периоди­чески, при этом выходной сигнал Y сдвинут по фазе на угол φ.

В любой произвольный момент времени кривые X и Y имеют разность ординат. Эта разность называется динамической погрешностью элемента. У большинства элементов абсо­лютная динамическая погрешность после скачкообразного воздей­ствия с течением времени не остается постоянной, а стремится к постоянному достаточно малому установившемуся значению.

Как установить закономерность динамического режима работы элементов и описать математически характеристику переходного процесса? Метод анализа переходного процесса целесообразно рассмотреть на наиболее часто встречающихся элементах, которые описываются дифференциальным уравнением вида

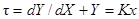(5.1)

где τ — постоянная времени; К — коэффициент пропорциональ­ности; х — величина входного сигнала.

В установившемся режиме Y = const и, следовательно, dY/dX=0.

С учетом этого из (5.1) получим уравнение статической харак­теристики такого элемента

Y=К'х. (5.2)

Пусть в момент времени t=0 входная величина изменилась скачкообразно от Х=0 до Х=Х, где Х— величина входного скач­кообразного сигнала (см. рис. 5.3). При Х=0 и Х=Х из уравне­ния (5.2) получаем, что установившееся значение выходной вели­чины до подачи скачкообразного сигнала было Y=0, а после по­дачи должно быть

. (5.3)

При t>0 X = x =const. С учетом уравнения (5.3) разделим пе­ременные dY/(Y—Y₀) = -dt/ τ. Проинтегрируем данное выражение

ln (Y— Y₀) —In С = -dt/τ или

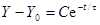(5.4)

где С — постоянная интегрирования, определяемая из начальных условий, т. е. при t = 0 и

Y =0. Подставив эти значения t и Y в (5.4), найдем C = -Y₀. Тогда выражение (5.4) примет вид

. (5.5)

Уравнение (5.5) — уравнение нарастающей, экспоненты и есть уравнение переходной характеристики для элементов, описываемых' дифференциальным уравнением вида (5.1).