Примеры решения задач в EXCEL
Основные правила при наборе формул в EXCEL
1. Для набора формул в EXCEL установите латинский шрифт (английский язык).
2. При наборе формул различий между строчными и прописными буквами нет.
3. Перед формулой ставится знак равенства.
4. Формулу можно копировать в ячейки стоящие справа, слева, выше, ниже. При копировании формулы вправо или влево автоматически меняется имя столбца, если необходимо чтобы имя столбца не менялось при копировании формулы, перед именем столбца ставится знак доллара ($). При копировании формулы вверх или вниз автоматически меняется номер строки, если необходимо чтобы номер строки не менялся, перед номером сроки ставится знак доллара ($).
5. Финансовые расчеты выполняются с точностью до второго знака после запятой, поэтому необходимо установить формат ячеек – числовой – два знака после запятой.
Порядок оформления решения задачи в WORD
1. Скопировать текст задачи из задания в соответствии с Вашим вариантом контрольного задания по финансовой математике.
2. Привести формулы, которые Вы намерены использовать для решения задачи. При наборе формулы использовать редактор формул WORD.
3. Расчет выполнить в EXCEL.
4. Лист EXCEL с расчетом скопировать при помощи клавиши Print Screen и вставить в программу Paint (Пуск 
программы стандартные Paint). После вызова программы Paint вставить лист EXCEL с расчетом двойным щелчком левой кнопки мыши (Paint – правка – вставить)
5. Со скопированного листа EXCEL вырезать часть, содержащую расчет, скопировать и вставить в текст WORD после, приведённых Вами расчетных формул.
Пример № 1:
Определить современную величину 100 тыс. руб., которую мы получим через год, через 2 года, и далее с шагом 1 год до 10 лет при использовании простых и сложных процентов 12 % годовых (проценты начисляются один раз в год, по полугодиям, ежеквартально, непрерывно).
1. Формулы для решения задачи:
а) дисконтирование по простой процентной ставке:
(1)
где S – сумма, которую мы получаем через год, через 2 года, и далее с шагом 1 год до 10 лет; P – современная величина суммы S, n – срок, r – простая ставка дисконтирования (десятичная дробь).
б) дисконтирование по сложной процентной ставке:
, (2)
где J – сложная процентная ставка дисконтирования (десятичная дробь),
m – число начислений процентов в году.
в) дисконтирование по непрерывной процентной ставке:
. (3)
где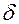 
- сила роста.
2. Порядок выполнения расчета в EXCEL:
1. В ячейку A1 вводим величину банковской процентной ставки (в долях от 1) 0,12.
2. В ячейку A2 вводим заданную сумму (100000), которую получим через год, через 2 года, и далее с шагом 1 год до 10 лет.
3. В ячейку B2 вводим цифру 1, в ячейку B3 цифру – 2, выделяем их (тем самым запоминаем шаг 1) и копируем до ячейки B11 (тоесть вводим цифры от 1 до 10 – это годы).
4. Устанавливаем курсор в ячейку C2 и вводим формулу дисконтирования по простой процентной ставке (1) =A$2/(1+a$1*B2) и копируем эту формулу вниз до ячейки C11.
5. Установим курсор в ячейку D1 и введем цифру 1, аналогично в ячейку E1 2, в ячейку F1 4 (введённые цифры – это количество начисления процентов в году).
6. Устанавливаем курсор в ячейку D2 и вводим формулу дисконтирования по сложной процентной ставке (2) =$a$2/(1+$a$1/D$1)^($b2*D$1) и копируем эту формулу вправо до ячейки F2 и затем вниз до ячейки F11.
7. Устанавливаем курсор в ячейку G2 и вводим формулу дисконтирования по непрерывной процентной ставке (3) =a$2/exp(a$1*b2) и копируем эту формулу вниз до ячейки G11.
8. Ячейки C2 
G11 выделяем и устанавливаем формат – цифровой (формат ячейки цифровой два знака после запятой).
9. Лист EXCEL с расчетом скопировать при помощи клавиши Print Screen и вставить в программу Paint (Пуск программы стандартные Paint). После вызова программы Paint вставить лист EXCEL с расчетом двойным щелчком левой кнопки мыши (Paint правка вставить)
10. Со скопированного листа EXCEL вырезать часть, содержащую расчет, скопировать и вставить в текст WORD.
Пример № 2:Нарицательная стоимость облигации со сроком погашения через 10 лет 1000 руб., купонная ставка: а) 10%, б) 11%. Проценты выплачиваются один раз в год. Рассчитайте текущую стоимость облигации, если рыночная доходность: а) 8%, б) 10%, в) 11%, г) 12%.
1. Формулы для решения задачи:
Текущая стоимость облигации определяется по формуле:
, (4)
где NOM – номинальная стоимость; n – cрок до погашения; KS - купонная процентная ставка; j – банковская процентная ставка; TSO – текущая стоимость облигации.
2. Порядок выполнения расчета в EXCEL:
1. В ячейку A1 вводим первую величину купонной процентной ставки (в долях от 1) 0,10.
2. В ячейку A2 вводим нарицательную стоимость облигации (1000), которую получим через 10 лет.
3. В ячейку B2 вводим цифру 1, в ячейку B3 цифру 2, выделяем их (тем самым запоминаем шаг 1) и копируем до ячейки B11 (тоесть вводим цифры от 1 до 10 – это годы).
4. В ячейку С1 вводим 0,08, в D1 0,10, в E1 0,11, в F1 0,12 – это заданные варианты банковской процентной ставки.
5. Устанавливаем курсор в ячейку C2 и вводим формулу для определения текущей стоимости выплат по купонам =$A$2*$a$1/(1+C$1)^$b2 и копируем эту формулу вправо до ячейки F2 и затем вниз до ячейки F11.
6. Ячейки C2 G11 выделяем и устанавливаем формат – цифровой (формат ячейки цифровой два знака после запятой).
7. Выделяем ячейки C2 С11 и левой кнопкой мыши щёлкаем по пиктограмме 
, определяем современную стоимость сумм, полученных по купонным выплатам (ячейка C12).
8. Устанавливаем курсор в ячейку C13 и вводим формулу для определения текущей стоимости номинала облигации, которую мы получим через n лет (в нашем примере n=10) =$a2/(1+c1)^$b11, копируем эту формулу вправо до ячейки F13.
9. Выделяем ячейки C12 С13, левой кнопкой мыши щёлкаем по пиктограмме , определяем современную стоимость сумм, полученных по купонным выплатам + современная сумма, полученная при гашении облигации (в ячейке с14),. копируем эту формулу вправо до ячейки F14.
10. Расчётная величина в ячейке D14 должна быть равна номиналу облигации (в нашем примере 1000), при равенстве величин купонной процентной ставки и банковской процентной ставки текущая стоимость облигации должна быть равна номиналу.
11. В ячейку A1 вводим вторую величину купонной процентной ставки (в долях от 1) 0,11. При этом расчет выполнится автоматически при новой величине купонной процентной ставки.
Пример № 3: Сравните два проекта (А и Б) по критериям чистый приведенный эффект (NPV) и внутренняя норма прибыли (IRR), , если цена капитала 15%. В проект А вкладываем (инвестируем) 20 тыс. руб. и ежегодно в течении 10 лет получаем дивиденды по 5 тыс. руб. В проект Б инвестируем 40. тыс. руб. В первый год получаем дивиденды 3.тыс. руб., во второй год 5 тыс. руб. и т.д. с нарастанием каждый год на две тыс. руб., в течении 15 лет.
1. Формулы для решения задачи:
Величина чистого приведённого дохода (NPV) определяется как разница сумм дисконтированных (по заданному значению банковской процентной ставке) величин доходов и инвестиций по годам:
Значение внутренней нормы доходности (IRR) определяется из условия равенства сумм дисконтированных (по значению внутренней норме доходности) величин доходов и инвестиций по годам:
где doxi – доходы по годам, ICi – инвестиции по годам, j – банковская процентная ставка, n – срок действия инвестиции.
2. Порядок выполнения расчета в EXCEL:
1. В ячейку A1 вводим заданную величину цены капитала (в долях от 1) 0,15.
2. В ячейку A2 вводим произвольную первоначальную величину внутренней нормы доходности проекта А (например 0,10).
3. В ячейку A3 вводим произвольную первоначальную величину внутренней нормы доходности проекта Б (например 0,10).
4. В ячейку B2 вводим цифру 0, в ячейку B3 цифру 1, выделяем их (тем самым запоминаем шаг 1) и копируем до ячейки B17 (то есть вводим цифры от 1 до 15 – это годы).
5. В ячейку С2 вводим заданное значение инвестиции в проект А -20000 в ячейки С3 С17 заданные значения доходов по годам по проекту А 5000.
6. В ячейку D2 вводим заданное значение инвестиции в проект Б -40000 в ячейки D3 3000 в ячейку D4 5000, выделяем их (тем самым запоминаем шаг 2000) и копируем до ячейки D17 (то есть вводим заданные значения доходов по годам по проекту Б).
7. Устанавливаем курсор в ячейку E2 и вводим формулу для определения текущей стоимости доходов и инвестиций по годам =C2/(1+$A$1)^$b2 и копируем эту формулу вправо до ячейки F2 и затем вниз до ячейки F17.
8. Ячейки D2 F17 выделяем и устанавливаем формат – цифровой (формат ячейки цифровой два знака после запятой).
9. Выделяем ячейки D2 D17 и левой кнопкой мыши щёлкаем по пиктограмме , определяем чистый приведенный эффект (NPV) проекта А (ячейка D18), копируем эту формулу вправо на ячейку F18, определяем чистый приведенный эффект (NPV) проекта Б (ячейка F18).
10. Устанавливаем курсор в ячейку H2 и вводим формулу для определения текущей стоимости доходов и инвестиций по годам при произвольно принятом значении IRR (0,1) для проекта А =H2/(1+A$2)^b2 и копируем эту формулу вниз до ячейки H17.
11. Ячейки H2 H17 выделяем и устанавливаем формат – цифровой (формат ячейки цифровой два знака после запятой).
12. Выделяем ячейки H2 H17 и левой кнопкой мыши щёлкаем по пиктограмме , определяем разницу сумм дисконтированных (по значению внутренней норме доходности) величин доходов и инвестиций по годам проекта А (ячейка H18), которая должна быть равна нулю при истинном значении IRR проекта А.
13. Устанавливаем курсор в ячейку I2 и вводим формулу для определения текущей стоимости доходов и инвестиций по годам при произвольно принятом значении IRR (0,1) для проекта Б =I2/(1+A$3)^b2 и копируем эту формулу вниз до ячейки I17.
14. Ячейки I2 I17 выделяем и устанавливаем формат – цифровой (формат ячейки цифровой два знака после запятой).
15. Выделяем ячейки I2 I17 и левой кнопкой мыши щёлкаем по пиктограмме , определяем разницу сумм дисконтированных (по значению внутренней норме доходности) величин доходов и инвестиций по годам проекта Б (ячейка I18), которая должна быть равна нулю при истинном значении IRR проекта Б.
16. Устанавливаем курсор на ячейку H18, вызываем программу «подбор параметра» (сервис подбор параметра), в появившемся окне устанавливаем значение 0, «изменяя значение ячейки $a$2 и левой кнопкой мыши щёлкаем по пиктограмме ОК, запускаем программу подбор параметра и определяем IRR для проекта А.
17. Аналогично определяем IRR для проекта Б.
Литература
а) Основная литература
1. Галиаскаров Ф.М., Муфтиев Г.Г., Бублик Н.Д., Кабирова А.С. Методы расчёта и математические модели финансовых операций. Уфа: Дизайн Полиграф Сервис, 2009. – 576с
2. Финансовая математика. Учебное пособие./Под редакцией академика А.Н. Романова. – М.: Вузовский учебник, 2007. – 359с
3. Четыркин Е.М. Финансовая математика – М.: Дело, 2005. – 400с
4. Кузнецов Б.Т. Финансовая математика. Учебное пособие – М.: Экзамен, 2005. – 128с
5. Малыхин В.И. Финансовая математика. Учебное пособие – М.: Юнити, 2004. – 237с
б) Дополнительная литература
1. Галиаскаров Ф.М., Мозалев А.А., Сагатгареев Р.М. Теория финансового менеджмента. Учебное пособие. – М.: Вузовский учебник, 2008. – 192с
2. Муфтиев Г.Г., Галиаскаров Ф.М., Теоретические основы финансового менеджмента. Учебное пособие. – Уфа: УИ РГТЭУ, 2007. – 230с
3. Финансовый менеджмент. Учебник. /Под редакцией академика Г.Б. Поляка. – М.: Юнити, 2006. – 527с
4. Галиаскаров Ф.М., Ахтямов Р.А. Финансовая математика. Учебное пособие – Уфа, 1999. – 130с
5. Р. Вейсвейллер. Арбитраж. Возможности и техника операций на финансовых и товарных рынках. М., Церих-Пэл, 1995.
6. Г.Г. Салыч. Опционные, фьючерсные и форвардные контракты. МГУ, 1994.
7. А.С. Чесноков. Инвестиционная стратегия, опционы и фьючерсы. М., НИИ Управления Мин. Экономики РФ, 1993.