СИНТЕЗ ПЛАНЕТАРНИХ ПЕРЕДАЧ
ДЗ: В тетрадь выпишите со стр. 94 11 ПРИЗНАКОВ, отличающих Человека от других видов животных.
Распределить события в истории живого мира и записать цифры в правильной последовательности по каждому этапу развития живой природы.
Цель: На материале истории развития живой природы НАУЧИТЬСЯ работать с текстом (развитие навыка смыслового чтения) и составлять логические цепочки.
А. Первичная эволюция п.14-15;
- Появление первых прокариот и водорослей;
- Формирование коацерватных капель и мембраны;
- Появление эукариот;
- Возникновение автотрофного питания;
- Синтез органических молекул из неорганических;
- Первые многоклеточные организмы и половой способ размножения;
- Возникновение дыхания;
Б. Морская эволюция п.16;
1. Расцвет морских беспозвоночных;
2. Появление конечностей
3. Развитие челюстного аппарата;
4. Появление животных с внутренним скелетом;
В. Эволюция растений на суше п.16-18.
1. Расцвет покрытосеменных;
2. Сокращение папоротников и голосеменных;
3. Псилофиты – первые наземные растения;
4. Возникновение семенного размножения и господство голосеменных;
5. Появление проводящей ткани растений
Г. Эволюция животных на суше п.16-18.
1. Появление первых насекомых;
2. Появление внутреннего оплодотворения и развития зародыша на суше;
3. Господство млекопитающих и птиц;
4. Появление человека;
5. Развитие грудной клетки и всасывающего типа дыхания;
6. Расцвет пресмыкающихся;
7. Стгоцефаллы;
Д. Эволюция Человека п.19-20
- Дриопитеки;
- Синантропы, питекантропы и гейдельбергские люди;
- Кроманьонцы;
- Появление насекомоядных млекопитающих
- Неандертальцы;
- Австралопитековые;
- Первые хищники и приматы;
Завданням синтезу планетарних передач є визначення чисел зубів коліс планетарної передачі за заданим передаточним відношенням.
Як і будь яке інженерне завдання, задача вибору чисел зубів коліс планетарної передачі не може бути вирішена абсолютно точно. З одного боку до механізму пред'являються вимоги по обмеженню габаритів і вагових показників, з іншого боку пред'являються вимоги до міцності ланок механізму і його точності. У загальному машинобудуванні вважається за достатню точність в межах похибки в 7%.
Виконуючи синтез планетарного редуктора, ми повинні задовольнити ряд вимог, які витікають з умов проектування механізму:
1) умова співвісності;
2) умова сусідства;
3) умова складання.
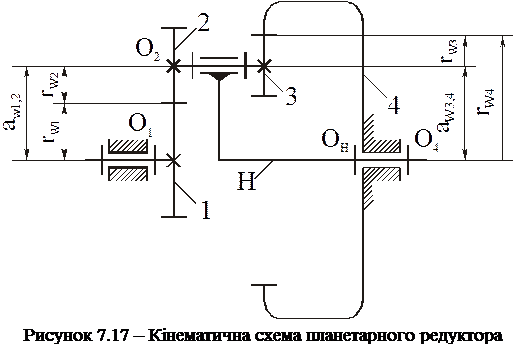 |
Розглянемо завдання синтезу на конкретному прикладі. Маємо слідуючи вихідні дані: кінематична схема редуктора (рисунок 7.17) і надане передаточне відношення U1,Н.
I. Визначаємо числа зубів коліс по передаточному відношенню. Для цього запишемо формулу передаточного відношення від першої ланки до водила через числа зубів, використовуючи метод Віліса:
 ,
,
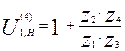 . (7.13)
. (7.13)
Звідки

Таким чином, ми отримаємо вираз для підрахунку чисел зубів коліс планетарного механізму, необхідних для забезпечення заданого передаточного відношення. Очевидно, що для задоволення заданного значення передаточного відношення можна отримати безліч поєднань чисел зубів, але однієї цієї умови недостатньо для вибору чисел зубів механізму. Окрім цієї умови мають бути витримані деякі інші обов'язкові умови.
II. Умова співвісності.
Розглянемо одну з необхідних умов, яку необхідно задовольнити при виборі варіантів поєднань чисел зубів коліс планетарного механізму.
Для того, щоб зубчате зачеплення працювало нормально, необхідно щоб геометричні вісі центральних коліс збігалися з геометричною віссю обертання водила. Ця умова здійснима, якщо міжвісьові відстані О1О2 і О4О2 дорівнюють
 .
.
Запишемо цю рівність через радіуси початкових кіл коліс:
 .
.
Зазвичай модуль всіх коліс планетарного редуктора однаковий. Хай всі колеса механізму нарізані без зсуву. В цьому випадку радіуси початкових кіл дорівнюють радіусам ділильних кіл. Тоді радіуси початкових кіл можуть бути визначені через числа зубів коліс
 ,
,
звідки отримаємо умову співвісності через шукані числа зубів:
 (7.17)
(7.17)
Отримане рівняння справедливе, якщо модулі всіх коліс однакові. Якщо ж модулі першої і другої пар зубів неоднакові (у першої m1, а у другої m2) , то це необхідно врахувати коефіцієнтом  , тоді умова співвісної для заданої схеми набирає вигляду:
, тоді умова співвісної для заданої схеми набирає вигляду:
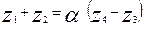 .
.
Ми отримали два рівняння (7.14) і (7.17) для вибору чисел зубів коліс механізму, а невідомих - чотири. Використовуючи рівняння (7.14) і (7.17)] можна підібрати раціональні варіанти чисел зубів, грунтуючись на деяких прийомах.
Умови (7.14) і (7.17) є обов'язковими для вибору чисел зубів. Окрім умов задоволення співвісної і передаточного відношення є додаткові умови, по яких проводиться перевірка вибраного варіанту співвідношення чисел зубів механізму: умова сусідства і умова складання.
Якщо сателіт один, то умови сусідства і складання виконуються автоматично і ці перевірки не потрібні. Як правило, планетарні передачі не роблять з одним сателітом; механізм з одним сателітом виходить неврівноваженим (незбалансованим). Для урівноваження блоку сателітів з протилежного боку на водилі необхідно розміщувати масу, що врівноважує масу блоку сателітів. Найзручніше для урівноваження з протилежного боку розмістити такий же блок сателітів. Як правило, в планетарних передачах на рівних кутових відстанях встановлюють 2, 3, 4 геометрично подібних блоків сателітів. При цьому планетарний механізм отримує наступні переваги:
1) система виходить урівноваженою (з одним сателітом центр тяжіння зміщений, з 2, 3, 4 - центр тяжіння системи знаходиться в геометричному центрі обертання сателітів);
2) центральні колеса зачіпляються з декількома сателітами і відбувається розподіл окружного зусилля (навантаження) між сателітами:
 ,
,
тут Р - повне окружне зусилля в передачі;
k - число сателітів.
Це можливо, коли навантаження між всіма сателітами розподіляється рівномірно. Практично в більшості випадків число сателітів k приймається рівним 3.
У зв'язку із зменшенням окружних зусиль зубчаті колеса мають менший модуль, тобто зменшуються габарити передачі.
Разом з вказаними перевагами при установці числа сателітів більше одного, з'являються додаткові умови, які мають бути дотримані в планетарному редукторі.
III. Умова сусідства
Умова сусідства полягає в тому, що сусідні сателіти не повинні зачіплятися один з одним. Якщо k =2, то сателіти розташовуються симетрично один по відношенню до одного - з протилежних сторін по відношенню до центру обертання водила і тому не можуть стикатися один з одним. Таким чином, перевірка на умову сусідства при k =2 не потрібна. При k >2 сателіти можуть стикатися один з одним, і щоб уникнути цього, необхідна перевірка на умову сусідства. Якщо сателітом є блок з 2х коліс, то перевірка виконується по колесу більшого діаметру.
Хай в нашому прикладі (рисунок 7.17) в блоці сателітів 2-3 колесо 2 більше колеса 3. Колесо 2 зачіпляється з колесом 1. Зобразимо другу проекцію цього зачеплення (початкові кола). Якщо ми маємо число сателітів k, то з'єднавши променями вісь обертання центрального колеса О1, з центром сусідніх сателітів О2 і О2', отримаємо центральний кут між двома сусідніми сателітами О2О1О2' рівний  (рисунок 7.1).
(рисунок 7.1).
З'єднаємо центри сателітів прямою лінією О2О2' і з осі обертання центрального колеса О1 опустимо перпендикуляр О1К на цю лінію. Отримаємо рівні відрізки О2К=О2'К.
З прямокутного трикутника О1КО2 знаходимо відрізок О2К
 .
.
Відрізок О1О2 є міжосьовою відстанню коліс 1 і 2:
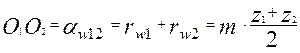 ,
,
Тоді  .
.
Розглянемо, якою має бути відстань О2О2' між центрами сусідніх сателітів, щоб їх зуби не стикалися. З малюнка 3 видно, що ця відстань має бути не менше двох радіусів кіл виступів сателітів - ra2. Для нульових коліс
Для нульових коліс
 .
.
Таким чином умову сусідства можна записати у вигляді
 .
.
Підставимо в цю нерівність значення, отримані раніше

У остаточному вигляді отримаємо
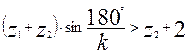 .
.
Ми отримали умову сусідства для сателітів, які мають зовнішнє зачеплення з центральним колесом. Якби ми розглядали умову сусідства для нашого прикладу сателітів, що мають внутрішнє зачеплення, то з урахуванням того, що міжвісьова відстань в цьому випадку О1О2 була б не сумою, а різницею радіусів початкових кіл, то, провівши дослідження аналогічні проведеним вище, отримаємо
 .
.
IV. Умова складання
Для того, щоб механізм був збалансований, блоки сателітів встановлюють симетрично. При установці сателітів зуби їх не повинні деформуватися і точно збігатися із западинами центральних коліс.
Для виконання умови складання планетарного механізму необхідно враховувати ряд конструктивних особливостей механізму:
1) блоки сателітів встановлюються тільки на рівних відстанях один від одного;
2) всі блоки сателітів геометрично подібні (орієнтація коліс 2, 3 у всіх блоках однакова);
3) сателіти з валом (зубчаті колеса 2 і 3) сполучені жорстко і не провертаються один щодо одного.
Якщо ми хочемо, щоб зуби сателітів точно збігалися із западинами центральних коліс, необхідно витримати певні співвідношення між числами зубів центральних коліс і коліс сателітів - це і буде умовою складання.
Розглянемо умову складання на прикладі планетарного механізму, зображеного на рисунку 7.17. Зобразимо другу проекцію центральних коліс 1 і 4 (рисунок 7.17). Припустимо, що нам необхідно встановити 2 блоки сателітів між колесами 1 і 4. Хай виявилось, що колеса 1, 4 зорієнтовані таким чином, що вгорі зуб колеса 4 встановлений напроти зуба колеса 1, а внизу - зуб колеса 4 проти западини колеса1. Якщо вгорі ми зможемо встановити блок сателітів 2, 3, то внизу це виявиться неможливим. Сателіти геометрично подібні і тому необхідно, щоб орієнтація зубів коліс 1 і 4 була внизу і вгорі однакова.
Перший сателіт можна завжди встановити, зорієнтувавши колеса 1 і 4 так, як це необхідно. Коли перший сателіт встановлений, колеса 1 і 4 взаємно зорієнтовані, тобто ми вже не можемо отримати будь-яке взаємне розташування їх зубів, оскільки орієнтація коліс тепер вже залежитиме від сателіта.
Розглянемо, коли ми зможемо встановити 2й сателіт на місце 1го. Якщо не враховувати умову сусідства, то теоретично наступний сателіт ми можемо встановити повернувши колесо 1 на один крок, тобто на кут

При повороті колеса 1 на кут j1 обернеться і водило Н, оскільки перший блок сателітів вже встановлений. Визначимо на який кут обернеться водило Н при повороті колеса 1 на кут j1 , скориставшись передаточним відношенням.

 .
.
Звідси визначимо кут повороту водила
 .
.
|
Таким чином теоретично можливе число сателітів Е ми можемо визначити, розділивши 2p на кут повороту водила jН при повороті першого колеса на кут j1.
 .
.
Припустимо, що нам необхідно встановити k сателітів - ціле число.
Розділивши теоретично можливе число сателітів Е на необхідне нам число сателітів k, отримаємо деяке число g
 ,
,
Де k - число сателітів - ціле число;
Е - теоретично можливе число сателітів - теж ціле число;
g - будь-яке ціле число.
Підставимо набутого значення Е в попередню формулу
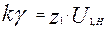 .
.
Отримаємо умову складання для планетарного механізму в загальному вигляді. Права частина рівняння має бути кратною числу сателітів k.
Визначимо умову складання планетарного механізму, зображеного на рисунку 7.17.
Визначимо передаточне відношення за формулою Вілліса:
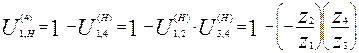 ,
,
 .
.
Записуємо умову складання:
 .
.
У остаточному вигляді отримаємо
 .
.
Як правило, число сателітів k дорівнює 3. Три сателіти саморозташовуються і контактують з колесами в 3х точках. Відбувається рівномірний розподіл навантаження між сателітами.
