Движение планет. Законы Кеплера. Параллакс

Задание № 3

Задача №2

Задача №1

Системы измерения времени в астрономии

Задание № 2

Задача №3

Задача №2

Задача №1

Системы координат. Видимое движение Солнца

Задание № 1

КОНТРОЛЬНАЯ РАБОТА

по дисциплине«АСТРОНОМИЯ»

Выполнили: ст. гр. ПГ1

ст.б. 3-12-26390

Кобец Е.Н

Вариант 30

Новосибирск 2013

Нарисовать основные точки, круги и линии небесной сферы. Изобразить небесную сферу в проекциях на плоскости небесного горизонта, небесного экватора и небесного меридиана.

Решение:

Небесная сфера – это воображаемая сфера произвольного радиуса, в центре которой находится точка наблюдения. На эту сферу проектируются положения всех небесных тел.

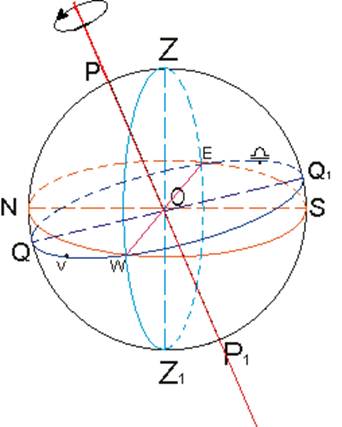
O – центр сферы точки состояния

наблюдения

Z – точка пересечения небесной сферы

отвесной линии (зенит)

Z₁- надир

ZZ₁- отвесная линия

NS- полуденная линия NS┴ ZZ₁

N- север

S- юг

PP₁- ось вращения небесной сферы и

совпадает с осью вращения земли

Р – северный полюс

Р₁- южный полюс

QQ₁ ┴ PP₁

QQ₁- экватор

E- запад

W- восток

Плоскость небесного экватора параллельна плоскости земного экватора. Небесным экватором называется плоскость проходящая через центр земли и перпендикулярно оси вращения небесной сферы.

Плоскость меридиана – называется плоскость, которая в сечении с небесной сферой дает круг PZQ₁SP₁Z₁QN.

Плоскость небесного горизонта – плоскость проходящая через центр небесной сферы и перпендикулярна отвесной линии.

Плоскость паралеи – это плоскость параллельна плоскости небесного горьзонта.

Плоскость вертикала – это плоскость проходящая через отвесную линию

Первый вертикал – от перпендикуляра плоскости меридиана

Плоскость круга склонения называется плоскость проходящая через ось вращения небесной сферы.

γ ОВЕН – 21 марта точка весеннего равноденствия

Ω ВЕСЫ – 23 сентября точка осеннего равноденствия

Угол наклона оси мира к горизонту равен географической широте (φ) места наблюдения (т. е. высота полюса мира hp над горизонтом равна географической широте места наблюдения, hp =φ).

Сделать чертежи горизонтальной и экваториальных систем координат. Нанести на них астрономический объект по заданным координатам своего варианта.

Решение:

1. Горизонтальная система координат

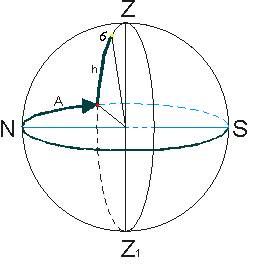
А=270^о, h= 80^o

2. Первая экваториальная система координат

δ= 0; t = 12^h = 180^o.

3. Вторая экваториальная система координат

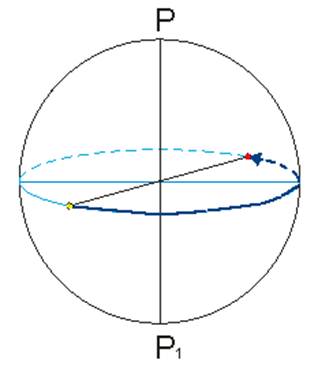δ= 0; α = 12^h = 180^o.

Нанести на чертеже небесной сферы точки, где находится Солнце в дни солнцестояний и равноденствий, а также примерное расположение Солнца на дату варианта.

Решение:

Дата 7.12

Солнце в дни солнцестояний:

К – 22.06 день летнего солнцестояния

К₁ – 22.12 день зимнего солнцестояния

γ – 21.03 день весеннего равноденствия

Ω – 23.09 день осеннего равноденствия

σ – 7.12 день примерного расположения Солнца

Определить всемирное время UT, поясное время T_n и декретное время D_n, соответствующие моменту местного среднего солнечного времени m на дату d в пункте с долготой λ .

Дано:

m = 10^h 57^m 39,509^s

λ = 8^h 12^m 03,27^s

d = 28 июля

D_n = 7^h 57^m 39,45^s

Найти:UT, T_n, D_n = ?

Решение:

В соответствии со значением долготы пункта наблюдения, номер пояса n = 8.

Для решения задачи воспользуемся формулой

Dn = Tn + k = UT + (n + k) = m - λ + (n + k),

где k = 1, если время зимнее, и k = 2, если время летнее.

m-λ=UT T_n=UT+n

m - λ	10^h 57^m 39,509^s 8^h 12^m 03,27^s
UT + n	2^h 45^m 36,239^s 8^h
T_n + k	10^h 45^m 36,239^s 2^h
D_n	12^h 45^m 36,239^s

Ответ:UT = 2^h 45^m 36,239^s

T_n =10^h 45^m 36,239^s

D_n = 12h 45^m 36,239^s

Определить местное среднее солнечное временя m, соответствующее декретному времени D_n на дату d в пункте с долготой λ.

Дано:

d = 28 июля

D_n = 7^h 57^m 39,45^s

λ = 8^h 12^m 03,27^s

Найти:m = ?

Решение:

Dn = Tn + k = UT + (n + k) = m - λ + (n + k) => m = Dn - (n + k)+λ

где k = 1, если время зимнее, и k = 2, если время летнее.

D_n - n+k	7^h 57^m 39,45^s 8+2=10^h
UT + λ	21^h 57^m 39,45^s 8^h 12^m 03,27^s
m	6^h 09^m 43,12^s

Ответ: m = 6^h 09^m 43,12^s