Пример 1.1.

ПАРАЛЛАКТИЧЕСКИЙ ТРЕУГОЛЬНИК СВЕТИЛА И ЕГО РЕШЕНИЕ

А

Вторая экваториальная система координат

Эта система также ориентирована на ось мира.

Основными её кругами являются небесныйэкватор и меридиан точки Овна. Точка Овна (γ) — это точка на небесном экваторе, в которой Солнце, перемещаясь в течение года по небесной сфере среди звезд, оказывается 21 марта. Эту точку также называют точкой весеннего равноденствия.

Координатами во второй экваториальной системе, которая показана на рис. 1.3,

являются склонение δи прямое восхождение а. Склонение является общей координатой для первой и второй экваториальных систем.

Прямым восхождением называется дуга небесного экватора, заключённая между меридианами точки Овна и светила. Прямое восхождение измеряется дугой небесного экватора от точки Овна навстречу западным часовым углам до меридиана светила в пределах от 0° до 360°.

Часто используют также дополнение прямого восхождения до 360°, которое называют звёздным дополнением:

Точка Овна участвует вместе со всеми светилами в суточном вращении небесной сферы.

Поэтому прямое восхождение, как и склонение, не зависит от вращения Земли. Это обстоятельство позволяет публиковать все каталоги звёзд в этой системе координат.

Звёздные дополнения и склонения 160 навигационных звёзд даны в МАЕ. В этой же системе координат нанесены звёзды на звёздный глобус.

Параллактическим треугольником называется сферический треугольник, вершинами которого являются: повышенный полюс мира, зенит и светило.

 

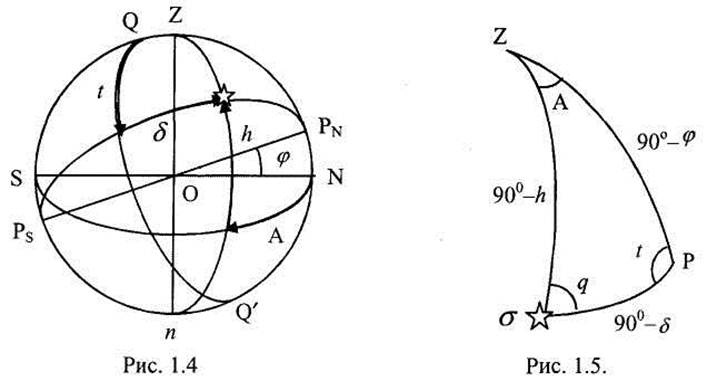
На рис. 1.4 видно, что параллактический треугольник образуется дугами меридиана наблюдателя, меридиана светила и вертикала светила. Его элементами являются стороны: зенитное расстояние, полярное дополнение и дополнение широты до 90°, а также углы: азимут при зените, часовой угол при повышенном полюсе мира и параллактический угол при светиле, из-за которого треугольник и называется параллактическим. Отдельно треугольник и его элементы показаны на рис. 1.5.

Решить треугольник - означает по заданным элементам найти другие. Для однозначного решения должны быть заданы три элемента. В зависимости от решаемой задачи могут быть заданы различные элементы. В основной же задаче, в которой используется параллактический треугольник, заданы:

φ, δиtм, а надо найтиh и А.

Треугольник решается на основании теорем сферической тригонометрии, которые в данном случае приводят к формулам:

 

Решение по этим формулам производится с помощью микрокалькулятора. Результат решения для высоты записывается с точностью до 0,'1, а для азимута - с точностью до 0,1°.

Знаки аргументов в формулах (1.1) и (1.2) следующие: φи tвсегда имеют знак «+»,

а δ«+», когда одноимённо с φи «-», если разноимённо.

По формуле (1.2) азимут получается в полукруговом счете. Его первая буква одноимённа с широтой, а вторая - с практическим часовым углом. Если азимут получился отрицательным, к нему добавляют 180°, а после этого присваивают наименование. Полученный полукруговой азимут необходимо перевести в круговой.

Решение. Вводим в микрокалькулятор φи t с плюсом, а 8 —с мину­сом. После вычислений без промежуточных записей получаем:

Пример 1.2.

Решение. Все- аргументы вводим с плюсом. После вычислений получаем:

Чтобы облегчить перевод азимута из одной системы в другую, полезно схематично изобразить картушку компаса, которая оцифрована в круговом счёте, и на ней, отложив заданный азимут, переводить его в другой счёт. В приложении 12 приводится программа для программируемого калькулятора Casio fx-6300G , с помощью которой треугольник решается за 15-20 секунд. До появления калькуляторов были разработаны десятки различных таблиц специально для решения параллактического треугольника. Некоторые из этих таблиц описаны в разделе 2.3.