Следующий большой этап работы связан с определением видимых с Земли координат Солнца.

О,830 b= 0о,300

E2 = M + 57о,296 ×e× sin Е1

E1 = M + 57о,296× e× sin М

Втрое приблизительное решение находим, подставляя под знак синуса Е1:

Совершенно аналогично находим третье, четвёртое и т.д. приближения.

Мы получим ряд сходящихся значений. Такие вычисления будем производить до тех пор, пока разница между двумя последними приближениями не будет меньше или равна нужной нам точности расчётов. Мы договорились все промежуточные величины считать с точностью 0^о,1. Значит, вычисления будем продолжать до тех пор, пока разница между двумя последними приближениями не будет меньше (или равна) 0^о,1. Последнее из приближений считаем окончательным.

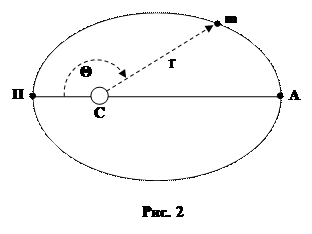
· Следующий этап работы – определение полярных координат планеты на момент определения. Напомню, что полярными координатами тела называются два числа, определяющие его положение на орбите. Это Θ – истинная аномалия планеты и r- радииус-вектор планеты ( см рис.2)

Здесь :

С – Солнце,

m – планета,

П – перигелий орбиты,

А– афелий орбиты,

Θ - истинная аномалия планеты,

r- радиус вектор планеты.

Истинная аномалия – Θ - это угол с вершиной в центре Солнца между направлением на перигей и на планету. Он всегда измеряется в сторону движения планеты вокруг Солнца от направления на перигей.

Радиус – вектор – r - это расстояние между центрами Солнца и планеты.

Связь между этими двумя величинами - это уравнение эллипса в полярных координатах:

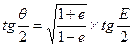(6)

Определение полярных координат начинается с определения истиной аномалии планеты:

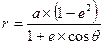(7)

Из уравнения (6) находим величину истиной аномалии, затем из уравнения ( 7 ) – радиус-вектор Юпитера.

· Далее находится промежуточная величина – U – аргумент широты планеты:

U° = L° + Θ° - M° - Ω°(8)

· Знание этой величины позволяет рассчитать гелиоцентрические эклиптические координаты планеты: гелиоцентрическую эклиптическую долготу - ℓ - и гелиоцентрическую эклиптическую широту – b – планеты. Фактически мы определяем, где будет видна планета относительно плоскости эклиптики и направления на точку весеннего равноденствия, если мы будем смотреть на неё из центра Солнца.

Сначала из ниже приведенного уравнения находим величину ℓ.

tg (ℓ - Ω) = cos i × tg U(9)

Сразу необходимо отметить, что при решении этого уравнения совершается больше всего ошибок. Дело в том, что величину (ℓ - Ω) мы определяем через обратную тригонометрическую функцию arc tg. Машина или калькулятор выдадут нам одно значение. Второе, исходя из знаков тангенса по четвертям, мы присваиваем сами.

Мы получим два значения величины (ℓ - Ω)^′ и (ℓ - Ω)^″. Из этих двух значений выбираем то, которое лежит в одной четверти сU. После этого определяем величину ℓ.

Далее находится вторая координата – эклиптическая гелиоцентрическая

широта - b , при этом здесь проблемы выбора из двух значений не будет. Мы получим сразу нужное нам значение.

sin b = sin U × sin i (10)

Здесь часто встречаются следующая ошибка. Некоторые студенты, получив отрицательное значение угла, согласно привычной процедуре прибавляют 360 градусов, приводя его значение к диапазону 0 – 360 градусов. В данном случае это не верно. Дело в том, что эклиптическая широта, так же как и географическая широта изменяется в пределах от -90 до +90 градусов.

В этом месте Вам выдаются первые промежуточные результаты, позволяющие проверить правильность решения пробной задачи. Если все сосчитали правильно, у Вас должно получиться:

Последовательно определяются следующие величины:

Здесь e_з= 0,0167 – эксцентриситет орбиты Земли.

В этом месте Вам выдаются вторые промежуточные результаты, позволяющие проверить правильность решения. Если все сосчитали правильно, у Вас должно получиться: