Итак, определим экваториальные координаты Юпитера 10 июня 2002 года.
К вычислению юлианского дня нужно подходить очень внимательно – это исходная величина для всех последующих вычислений. Если Вы рассчитаете её неправильно, вся дальнейшая шестичасовая работа окажется напрасной. Поэтому, прежде чем приступать к выполнению лабораторной работы, выполните контрольные вычисления юлианского дня по обоим алгоритмам для даты, например, 10 июня 2002года. В обоих случаях у Вас должно получиться, что JD = 2452435,5.
G = G , если М ≥ 3 ; m = M + 1 , если М ≥ 3 .
G = G – 1 , если М < 3 ; m = M + 13 , если М < 3 .
Рис. 1 Элементы планетных орбит.
Теория вопроса.
Термин «эфемерида» в общем смысле этого слова используется в астрономии для обозначения расчётных значений каких-либо величин для любого астрономического события. Например, в эфемериде Солнечного затмения на какую-либо дату и для какого-то населенного пункта, указываются времена начала и конца затмения в этом населённом пункте, значение максимальной фазы затмения, взаимные положения Солнца и Луны в моменты начала и конца затмения и многое другое.
В нашем случае, под эфемеридой какого либо тела Солнечной системы мы будем понимать рассчитанные значения только экваториальных координат этого тела для определённой даты года. Напомню, что экваториальные координаты светила это прямое восхождение (α) и склонение (δ). Их знание позволяет построить положение светила на звёздной карте, а значит, решать многие задачи связанные с определением условий видимости этого тела.
Исходными данными для решения этой задачи являются элементы орбиты интересующего нас объекта.
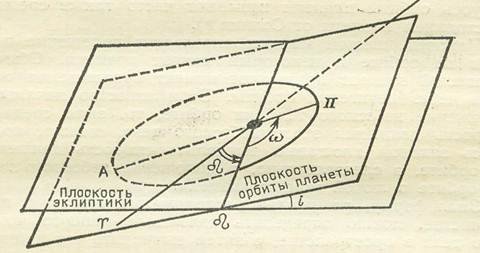
Элементами орбиты планеты называют шесть чисел, которые определяют положение планеты в пространстве относительно плоскости орбиты Земли (плоскости эклиптики) и направления на точку весеннего равноденствия.
Это следующие величины (см. рис. 1):
1. L - средняя долгота планеты для определённого момента времени. Знание этой величины позволяет рассчитать положение планеты на её орбите для любого другого момента времени. (На рис. не представлена.)
2. i - наклонение орбиты. Это угол между плоскостью орбиты планеты и плоскостью орбиты Земли.
3. Ω - долгота восходящего узла. Это угол с вершиной в центре Солнца между направлением на точку весеннего равноденствия и на ту точку орбиты планеты, где она переходит из южной полусферы в северную. Напомню, что противоположная точка орбиты планеты, где она переходит из северной полусферы в южную, называется нисходящим узлом. На рисунке этот угол отмечен специальным знаком, которого нет в символах компьютера. Поэтому мы будем пользоваться другим обозначением - Ω .
Необходимо понимать, что эти два элемента – i и Ω задают пространственную ориентацию плоскости орбиты планеты относительно плоскости орбиты Земли и направления на точку весеннего равноденствия.
4. ω - долгота перигелия. Это угол между направлениями на восходящий узел и на перигелий орбиты. Фактически этот угол определяет ориентацию большой оси орбиты планеты в плоскости её орбиты.
5. a – большая полуось орбиты планеты (обычно в а.е.).
6. e – эксцентриситет орбиты. Последние два элемента определяют форму и размеры орбиты планеты.
Здесь важно понимать следующее. Не может быть двух различных тел солнечной системы, у которых имеется одинаковый набор элементов их орбит. Если бы такое случилось, это значило бы, что в любой момент времени эти два тела находились бы в одной точке пространства.
Именно поэтому набор элементов орбиты – это своеобразный «паспорт» данного тела, по которому мы отличаем его от других тел.
Дело несколько осложняется тем, что элементы орбит всех тел солнечной системы с течением времени медленно изменяются. В курсах астрономии их называют оскулирующими, т.е. изменяющимися.
Обычно любой элемент орбиты задаётся в виде полинома:
А = А0 + А1 Т + А2 Т2 + А3 Т3
где А – определяемое нами значение какого-либо элемента орбиты на момент времени Т;
А0 , А1, А2 и т.д.- некие численные константы, значение которых различны для разных тел;
Т - время, на которое рассчитывается эфемерида тела.
Мы не будем вычислять положения планеты очень точно (а это можно сделать с точностью до долей секунды дуги). Для достижения нужной нам точности расчётов достаточно первых двух членов разложений по степеням Т. Ограничимся точностью до 0О,1.Поэтому при расчете значений элементов орбит не будем учитывать члены полиномов, содержащие Т2 и Т3 . Элементы орбит планет солнечной системы, доступных для школьных наблюдений, приведены ниже.
| Меркурий | |
| L | 178о,179 + 149474о,071 × Т |
| a | 0,387 а.е. |
| e | 0,206 |
| i | 7о,003 + 0о,002 × Т |
| ω | 28о,754 + 0,37 × Т |
| Ω | 47о,146 + 1о,185 × Т |
| Венера | |
| L | 342о,767 + 58519о,212 × Т |
| a | 0,723 а.е. |
| e | 0,007 |
| i | 3о,394 + 0о,001 × Т |
| ω | 54о,384 + 0о,508 × Т |
| Ω | 75о,78 + 0о,9 × Т |
| Марс | |
| L | 293о,737 + 19141о,696 × Т |
| a | 1,524 а.е. |
| e | 0,093 |
| i | 1о,85 |
| ω | 285о,432 + 1о,07 × Т |
| Ω | 48о,786 + 0о,771 × Т |
| Юпитер | |
| L | 238о,049 + 3036о,302 × Т |
| a | 5,203 а.е. |
| e | 0,048 |
| i | 1о,309 - 0о,006 × Т |
| ω | 273о,278 + 0о,599 × Т |
| Ω | 99о,443 + 1о,011 × Т |
| Cатурн | |
| L | 266о,564 + 1223о,51 × Т |
| a | 9,555 а.е. |
| e | 0,056 |
| i | 2о,493 - 0о,004 × Т |
| ω | 338о,309 + 1о,085 × Т |
| Ω | 112о,79 + 0о,873 × Т |
В нашей лабораторной работе мы будем определять только экваториальные координаты: прямое восхождение (α ) и склонение (δ ) какой - либо планеты на определённую дату: D – число, M – месяц и G – год. Поскольку координаты планет в течение суток изменяются очень медленно, поэтому мы не будем учитывать их суточные изменения и не будем вводить в исходные данные часы и минуты какой- либо даты.
Отдельного разговора заслуживает величина Т.
По своему смыслу это промежуток времени от некоторого момента в далёком прошлом до того момента, на который мы рассчитываем координаты планеты. В наших расчетах за такой «нулевой» момент времени принимается полдень 1 января 1900 года. Может быть выбран и другой какой-то момент, но при этом изменятся некоторые формулы для расчётов координат планеты.
По ряду чисто исторических причин при решении таких задач время измеряют не в часах, минутах или секундах, а в юлианских столетиях - это количество суток содержащихся в сотне лет Юлианского календаря – 36525 суток. Такова своеобразная единица измерения времени, используемая при проведении многих расчетов в астрономии.
Сейчас попытаемся понять, как определяют количество таких «единиц» содержится в промежутке времени от полудня 1.1.1900 г. до нашей даты. Для этого придётся познакомиться с ещё одним непривычным для нас понятием – юлианский день.
Это понятие «работает» тогда, когда нужно точно определить, сколько времени прошло между двумя какими-либо событиями, далеко отстоящими друг от друга по времени. Задача особенно осложняется ещё и тем, что даты событий могут быть заданы в разных календарных системах.
Поэтому в астрономии моменты событий задаются не годом, месяцем, датой, часом и т.д., а так называемым юлианским днём.
Договорились о том, что начиная с далёкого момента в прошлом
(полдень 1 января 4713 года до нашей эры) астрономы просто стали считать сколько суток прошло до нужной даты не взирая ни на какие реформы и типы календарей. Это число прошедших суток стали называть юлианским днём. Таким образом, каждому году, месяцу и числу соответствует свой юлианский день. Это позволяет просто находить интервалы времени между двумя далёкими событиями – достаточно найти разницу их юлианских дней.
В астрономии используются два алгоритма нахождения юлианского дня по году, месяцу и дате. Ниже они приведены:
JD=367×G - INT(7×(G + INT((M+9)/12))/4)+INT(275×M/9)+D+1721013,5 (1)
Здесь:
G– номер года;
М – номер месяца;
D - число;
INT - оператор выделения целой части.
JD = INT(365,25×G) + INT(30,6 × m) + D + 1720981,5 (2)
Здесь:
Необходимо сделать два важных замечания:
2. Такие контрольные вычисления проводите, глядя на алгоритмы не на экране монитора, а на эти соотношения, переписанные в свою тетрадь. Только в этом случае можно быть уверенным в том, что эти и все последующие соотношения Вы переписали правильно, и с ними можно будет правильно работать в дальнейшем, тем более, что контрольную работу Вы будете выполнять не по этой методичке, а по записям в своей тетради.
Прежде чем выполнить зачётное контрольное задание, Вы должны провести все расчеты для какой-то планеты и конкретной даты, где Вам предоставляется возможность проверить некоторые промежуточные результаты и таким образом локализовать ошибку в расчетах, если она будет присутствовать.
Промежуточные контрольные результаты будут приводиться в этой методичке.
Это контрольный пример, где будут представлены некоторые промежуточные величины расчетов, чтобы Вы могли локализовать возникшие ошибки и успешно сделать контрольную задачу.
· Выполнение работы начинается с расчета юлианского этой даты дня по вышеприведённым соотношениям (1) и (2).
· По номеру юлианского дня рассчитывается величина Т – время. В дальнейшем мы будем называть эту величину временным аргументом:
T=(JD-2415020)/36525 (3)
Здесь:
JD – номер юлианского дня 10 июня 2002 года;
2415020 – номер юлианского дня полудня 1 января 1900 года.
36525– число суток в ста годах юлианского календаря.
Тогда можно понять, что Т – это время, прошедшее от полудня 1.1.1900 до 10июня 2002года, выраженное в часах, минутах и секундах, а в долях юлианских столетий.
Особенно важно то, что величину Т необходимо рассчитывать с точностью не менее, чем восемь – девять знаков после запятой. Что бы понять это, посмотрите, как будет рассчитываться, например, - L – средняя долгота Венеры:
L = 342о,767 + 58519о,212 × Т (см. таблицу элементов орбиты Венеры). Наш временной аргумент – Т - предстоит умножать почти на 60000 градусов. Следовательно, если мы хотим добиться точности в расчетах 0,1 градуса, необходимо величину Т задавать с точностью не менее, чем восемь значащих цифр после запятой.
Все остальные расчетные величины, как мы договаривались выше, мы будем рассчитывать с точностью трёх значащих цифр после запятой. Нет необходимости считать их с точностью, например, 6 или 8 значащих цифр. Вы только усложните и удлините все расчеты без особой необходимости.
Следующим этапом работы является расчет элементов орбиты Юпитера на нужную нам дату. Для этого используем данные об элементах орбиты этой планеты:
| Юпитер | |
| L | 238о,049 + 3036о,302 × Т |
| a | 5,203 а.е. |
| e | 0,048 |
| i | 1о,309 - 0о,006 × Т |
| ω | 273о,278 + 0о,599 × Т |
| Ω | 99о,443 + 1о,011 × Т |
Здесь нужно иметь в виду, что при вычислении элементов орбиты (особенно L ) у Вас может получиться значение много превышающее 360о. В таких случаях, полученное значение необходимо привести к диапазону 0о – 360о. Для этого полученное большое значение разделите на 360о, целую часть уберите, а дробную часть снова умножьте на 360о.
· На основании рассчитанных элементов орбиты, определяем величину М. Она носит непривычное для нас название – средняя аномалия планеты.
М = L – ω - Ω (4)
· Найденное значение М используем для определения эксцентрической аномалии планеты– Е. Связь между этими величинами задается уравнением Кеплера:
E = M +57о,296 × e× sin E (5)
Здесь:
57о,296 – величина одного радиана в градусах;
е – эксцентриситет орбиты Юпитера.
Уравнения такого типа называются трансцендентными – неизвестная нам величина - Е - присутствует и под знаком тригонометрической функции. Такие уравнения решаются методом последовательных приближений. Первое приблизительное решение - Е1 – находим, подставляя под знак тригонометрической функции синуса найденную нами ранее величину средней аномалии - М :