Интерполяционная формула Ньютона.

Пусть у_0, у_1, у_2,....... – значения некоторой функции y = f (x), соответствующие равноотстоящим значениям аргументам х₀, х₁, х₂, ....... (т.е. х_k+1 – x_k = Δx = const ).

Введем обозначения:

Δу₀ = у₁ – у₀, Δу₁ = у₂ – у₁, Δу₂ = у₃ – у₂, ......... , Δу_п-1 = у_п – у_п-1 - разности первого порядка данной функции;

Δ²у₀ =Δ у₁ –Δ у₀, Δ²у₁ =Δ у₂ –Δ у₁, ............. – разности второго порядка

........................................................................

Δ^п+1у₀ =Δ^пу₁ –Δ^пу₀, Δ^п+1у₁ =Δ^пу₂ –Δ^пу₁, ............. – разности (п+1)- го порядка

Производя последовательные подстановки, получим:

Δ²у₀ = у₂ -2у₁ + у₀ , Δ³у₀ = у₃ -3у₂ +3 у₁ – у₀ , ........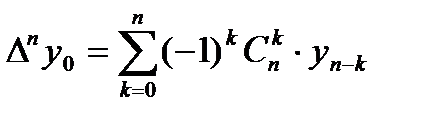

Подобным же образом получаем:

у₁ = у₀ + Δу₀ , у₂ = у₀ + 2Δу₀ + Δ²у₀ , у₃ = у₀ + 3 Δу₀ + 3Δ²у₀ + Δ³у₀ , ......

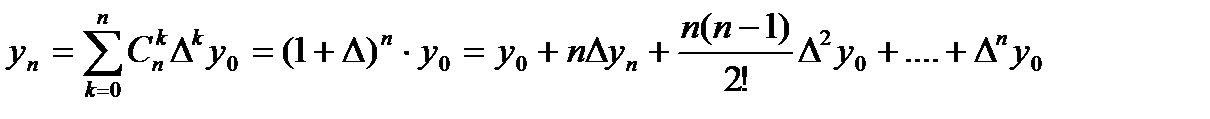(3)

Запишем таблицу разностей:

х₀ у₀

Δ у₀

х₁ у₁ Δ²у₀

Δ у₁Δ³у₀

х₂ у₂ Δ²у₁Δ⁴у₀

Δ у₂ Δ³у₁

х₃ у₃ Δ²у₂

Δ у₃

х₄ у₄

....................................................

Если в формуле (3) положить, что п – не только целое и положительное число, а может быть любым п = t, то получим интерполяционную формулу Ньютона

(4)

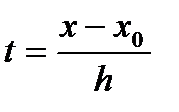Мы получили такую функцию от t, которая обращается при t = 0 в у₀, при t = 1 в у_1, при t = 2 в у₂ и т. д. Поскольку последующее значение аргумента х при постоянном шаге h определяется формулой x_n = x₀ + nh, то . Тогда, полагая x = x₀ + th , приведем формулу (3) к виду 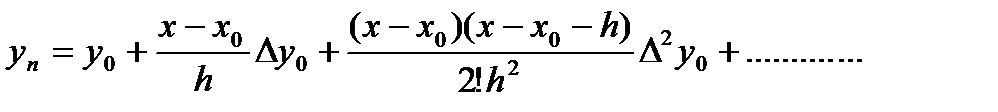(3^*)

х
у

Пример 2.2:

Из таблицы

Найти значение у при х = 3,1, пользуясь интерполяционной формулой Ньютона.

Решение.Составим таблицу разностей:

х	у	Δу	Δ2 у	Δ3 у

 

Здесь х₀ = 3, х = 3,1, h = 1. Тогда

Интерполяционная формула Ньютона (4) для этого случая:

Следовательно 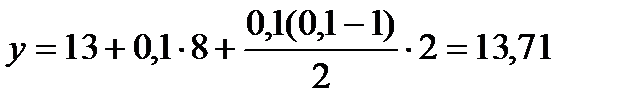, т.е. при х = 3,1 у = 13,71

Интерполяционная функция Ньютона (3^*)