III. Достаточное условие дифференцируемости
Теорема.Пусть функция 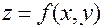 удовлетворяет условиям предыдущей теоремы:
удовлетворяет условиям предыдущей теоремы:
1. В окрестности точки  она имеет частные производные
она имеет частные производные  .
.
2. В самой точке  частные производные непрерывны.
частные производные непрерывны.
Тогда 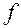 дифференцируема в точке
дифференцируема в точке  .
.
Доказательство.В силу условий теоремы справедлива формула (4) для полного приращения  :
:

 .
.
Для того, чтобы придти к представлению (2), входящему в определение дифференцируемости, положим
 .
.
Остается убедиться, что функция  является бесконечно малой более высокого порядка, чем
является бесконечно малой более высокого порядка, чем  . Имеем
. Имеем
 ;
;
при этом

и по свойствам бесконечно малых:  при
при  . ▄
. ▄