II. Формула для полного приращения

Теорема.Пусть функция 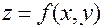удовлетворяет двум условиям:

1. В окрестности точки она имеет частные производные .

2. В самой точке частные производные непрерывны.

Тогда для полного приращения в точке справедлива формула :

, (4)

где частные производные вычислены в точке , а функции являются при и бесконечно малыми величинами.