VI.1. Векторный и скалярный потенциалы

Алехина Т.Ю.

Руководство к практическим занятиям «Электродинамика»

Часть VI

Электромагнитные поля, создаваемые ограниченными излучающими системами

 

Учебно – методическое пособие

 

Санкт – Петербург

2011 г.

Выше мы рассматривали задачи с не зависящими от времени электрическими и магнитными полями. В обоих случаях применялись аналогические математические методы, но электрические и магнитные явления рассматривались как независимые. Единственным связующим звеном был тот факт, что токи, создающие магнитные поля, имеют, по существу, электрическую природу, поскольку они обуславливаются движением электрических зарядов. При рассмотрении переменных во времени полей независимость электрических и магнитных явлений исчезает. В этом случае мы имеем не электрическое и магнитное поля в отдельности, а общее электромагнитное поле. Его поведение описывается системой уравнений Максвелла. Исследование этих уравнений и их решений позволяет изучить основные свойства электромагнитных волн и вопросы их распространения в различных средах и системах [1-6].

Данная часть настоящего пособия посвящена исследованию излучения электромагнитных волн ограниченными системами колеблющихся зарядов и токов. Если рассматривать только достаточно простые излучающие системы, то можно ограничиться сравнительно простым математическим аппаратом. Более систематическое изложение теории излучения можно посмотреть, например, в [1, гл. 19], где рассматриваются мультипольные поля.

VI.1. Векторный и скалярный потенциалы

Уравнения Максвелла (1.1) образуют систему взаимосвязанных уравнений первого порядка в частных производных, определяющих изменение составляющих электрического и магнитного полей. Для простых конфигураций они могут быть решены непосредственно. Однако часто удобно ввести потенциалы и свести систему к меньшему числу уравнений второго порядка. При этом некоторые из уравнений Максвелла удовлетворяются автоматически. Аналогичный подход использовался в электро- и магнитостатике (часть I).

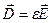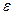Рассмотрим случай изотропной однородной среды, когда выполняются материальные соотношения , с постоянными и . Вводя в рассмотрение векторный и скалярный потенциалы и , которые определяются соотношениями

, . (6.1)

С учетом калибровки Лоренца 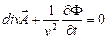, (6.2)

уравнения Максвелла могут быть сведены к неоднородным волновым уравнениям, называемым также уравнениями Даламбера [1, 2]

, (6.3)

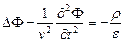, (6.4)

где 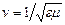, , 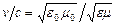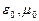- диэлектрическая и магнитная проницаемости вакуума, c - скорость света в вакууме. Здесь используется система единиц СИ.

Уравнения (6.3), (6.4) в совокупности с (6.2) образуют систему уравнений, полностью эквивалентных уравнениям Максвелла. Следует отметить, что Лоренцовская калибровка (6.2) является наиболее употребительной, поскольку, при ее использовании и входят эквивалентным образом в волновые уравнения и, кроме того, она не зависит от выбора координатной системы и потому очень удобна, например, в специальной теории относительности [1].

Условие Лоренца (6.2) не противоречит уравнению непрерывности . Так как заряды и токи независимы, то для расчетов удобно выразить их через одну функцию, выбранную так, чтобы уравнение неразрывности выполнялось тождественно:

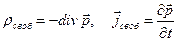. (6.5)

Вектор называется вектором поляризации. Совершенно аналогично векторный и скалярный потенциалы и можно выразить через единственную векторную функцию

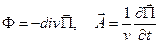. (7.6)

Условие Лоренца при этом выполняется автоматически. Вектор называется поляризационным потенциалом или потенциалом Герца [3] и удовлетворяет уравнению

(6.7).

Компоненты электрического и магнитного полей выражаются через вектор Герца с помощью соотношений

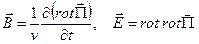. (6.8)

Заметим, что первое из соотношений (6.8) справедливо в общем случае, а второе – только вне источников поля.

Если воспользоваться разложением в интеграл Фурье по времени (П6.1)

, (6.9)

то можно записать уравнения Максвелла для Фурье – компонент полей в виде

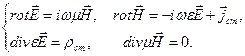(6.10)

Введя фиктивные магнитные источники и записав по аналогии с (6.5)

, (6.11)

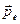где и 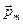- объемные плотности электрического и магнитного дипольных моментов соответственно, систему уравнений Максвелла (6.10) можно записать в виде двух систем уравнений для полей электрического и магнитного типов :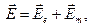

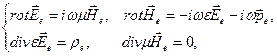(6.12)

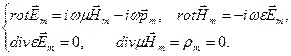(6.13)

При этом можно сформулировать так называемый принцип перестановочной двойственности 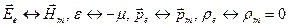. (6.14)

Далее, введем электрический и магнитный векторы Герца и , используя (6.6), (6.1),

, (6.15)

. (6.16)

Тогда потенциалы Герца и подчиняются уравнениям

, (6.17)

, (6.18)

где 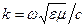- волновое число в среде, и - произвольные функции. Наличие этих функций связано с градиентной инвариантностью выражений (6.17), (6.18) для полей, значения которых не меняются при добавлении к векторам Герца градиента произвольной функции.

Упрощение математического описания электромагнитного поля достигается в криволинейных ортогональных системах координат , обладающих координатой разделения. Если таковой является 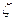, то коэффициенты Ламэ 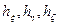подчиняются условиям

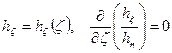. (6.19)

В однородной среде при выполнении условий (6.19) в области вне источников общее решение уравнения Максвелла дается суперпозицией двух фундаментальных решений, одно из которых описывается однокомпонентным электрическим, а другое магнитным векторами Герца, направленными по координате разделения. Первое из этих решений является поперечно – магнитным ТМ (или электрическим e), а второе – поперечно – электрическим ТЕ (или магнитным m) относительно координаты разделения . При этом потенциалы электрического и магнитного векторов Герца удовлетворяют каждая в отдельности одному дифференциальному уравнению второго порядка. Наличие у уравнений Максвелла двух фундаментальных решений, соответствующих ТМ- и ТЕ – полям, называется принципом поляризационной двойственности [4].