Прямоугольная изометрическая проекция окружности

 

Если построить изометрическую проекцию куба, в грани которого вписаны окружности диаметра D (рис. 76), то квадратные грани куба будут изображаться в виде ромбов, а окружности в виде эллипсов (рис. 76'). Надо запомнить, что малая ось С'D' каждого эллипса всегда должна быть перпендикулярна большой оси A'B'.

Если окружность расположена в плоскости, параллельной плоскости П₁, то большая ось А'B' должна быть горизонтальной, а малая ось С'D' – вертикальной (рис. 76).

Если окружность расположена в плоскости, параллельной плоскости П₂, то большая ось эллипса должна быть проведена под углом 90° к оси y. При расположении окружности в плоскости, параллельной плоскости П₃, большая ось эллипса располагается под углом 90° к оси х.

Заметим, что большие оси всех трех эллипсов направлены по большим диагоналям ромбов. При построении изометрической проекции окружности без сокращения по осям х, у и z длина большой оси эллипса берется равной 1,22 диаметра D изображаемой окружности, а длина малой оси эллипса – 0,71D (рис. 76).

В учебных чертежах вместо эллипсов рекомендуется применять овалы, очерченные дугами окружностей. Упрощенный способ построения овалов в плоскости, параллельной П₁. Проводят вертикальную и горизонтальную оси овала (рис. 76).

Из точки пересечения осей О проводят вспомогательную окружность диаметром D, равным действительной величине диаметра изображаемой окружности, и находят точки n пересечения этой окружности с аксонометрическими осями х и у.

Из точки m пересечения вспомогательной окружности с осью z, как из центра радиусом R = nm , проводят две дуги nDm и nСn окружности, принадлежащие овалу. Из центра O радиусом ОС, равным половине малой оси овала, засекают на большой оси овала АВ точки О₁ и O₂. Из этих точек радиусом r = O₁1 = O₁2 = O₂3 = O₂4 проводят две дуги. Точки 1, 2, 3, 4 сопряжений дуг радиусов Р и r находят, соединяя точки m с точками О₁ и О₂ и продолжая прямые до пересечения с дугами nСn и nDn. Также строят овалы, расположенные в плоскостях, параллельных плоскостям П₂ и П₃ (рис. 76).

Изометрия шара (рис. 77) выполняется следующим образом. Из намеченного центра О' проводят окружность диаметром, равным 1,22 (D – диаметр шара). Это и будет изображение шара в изометрии.

 

 

 

Рис. 76. Упрощенное построение овалов
в прямоугольной изометрической проекции

 

 

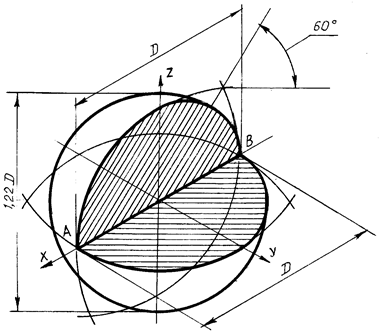
Рис. 77. Изометрическая проекция сферы с вырезом

 

 

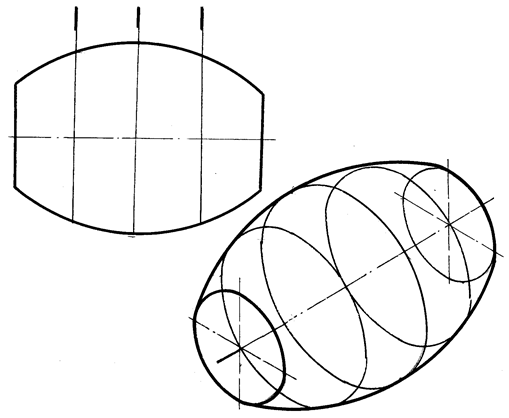
Рис. 78. Изометрическая проекция очерка тора,
выполненного методом сечений

Если требуется построить половину, четверть или три четверти шара, то необходимо сначала вычертить два овала (см. рис. 77), большие оси которых перпендикулярны осям у и z.

Тогда овалы и точки m и n пересечения этих овалов определят границы трех четвертей шара (рис. 77). Границей является окружность, касательная к этим овалам.