Алгоритм раскрытия статической неопределимости

 

Определение реакций в дополнительных связях называют рас­крытием статической неопределимости. Выполняется оно по единому алгоритму, который состоит из следующих шагов.

1. Определение степени статической неопределимости.

2. Выбор основной системы (ОС).

3. Переход к эквивалентной системе (ЭС).

4. Составление системы канонических уравнений.

5. Вычисление коэффициентов при неизвестных и свободных чле­нов уравнений. Решение системы канонических уравнений.

6. Построение суммарных эпюр внутренних силовых факторов.

7. Проверка правильности раскры­тия статической неопределимости.

 

Рассмотрим содержание этих шагов.

Определение степени статической неопределимости.Разность между общим числом внешних и внутренних связей, наложенных на систему (С_о), и числом связей, необходимых для ее равновесия (С_н), называется степенью статической неопределимо­сти (L)

 

L = Cо – Cн .*

(3.9)

 

Иными словами, L равна числу дополнительных связей, наложенных на систему.

При определении С_о плоской стержневой системы необходимо учитывать, что:

- бесшарнирный контур, включенный в систему, дает три дополни­тельные связи;

 

 

* Формула введена автором

- шарнир, соединяющий два стержня (одиночный шарнир), снижает степень статической неопределимости на единицу (устраняет одну связь);

- шарнир, в котором сходится n стержней, устраняет n-1 связей, т.е. заменяет собой n-1 одиночных шарниров.

Число связей, необходимых для равновесия системы (С_н), равно:

- 1 для линейной системы, т.е. системы, у которой все стержни и все нагрузки находятся на одной линии;

- 3 для плоской системы, т.е. системы, у которой все стержни и все нагрузки находятся в одной плоскости;

- 6 для пространственной системы, т.е. системы, у которой стержни и нагрузки произвольным образом расположены в про­странстве.

В некоторых учебниках по дисциплине «Сопротивление материалов» для определения степени статической неопределимости плоской сис­темы дается формула типа

 

L = 3К – Ш ,

(3.10)

 

где К – общее число замкнутых контуров; Ш – общее число шарниров в пересчете на одиночные.

Выбор основной системы.Основной называется статически определимая, геометрически и кинематически неизменяемая система, полученная из заданной ста­тически неопределимой системы путем освобождения ее от дополни­тельных связей и заданной нагрузки.

Внешние дополнительные связи, как правило, убирают, а для освобождения от внутренних вводят шарниры или производят раз­резы. Для обеспечения кинематической неизменяемости необходимо, чтобы направления всех связей, оставленных в качестве необходимых, не пересекались в одной точке или не были параллельны.

Следует иметь в виду, что для любой статически неопределимой системы можно выбрать несколько основных (как минимум две). Из всех возможных ОС для расчета рекомендуется выбирать наиболее рациональную. Рациональность ОС определяется трудоемкостью решения с ее использованием. Чем проще строить эпюры внутренних силовых факторов, чем на меньшем числе участков они располага­ются, тем рациональней ОС. Использование свойств симметричных расчетных схем позволяет уменьшить число канонических уравне­ний, использовать в качестве ОС половину, а иногда и меньшую часть расчетной схемы.

Переход к эквивалентной системе. Эквивалентной называется система, полученная из основной пу­тем нагружения ее заданной нагрузкой и неизвестными усилиями (реакциями) Х_i взамен отброшенных дополнительных связей. В тех точках, где были запрещены линейные перемещения, прикладывают сосредоточенные силы, а там, где были запрещены угловые переме­щения, – сосредоточенные моменты. Усилия Х_i прикладывают по на­правлению отброшенных связей.

Запись системы канонических уравнений.Общая форма записи таких уравнений следующая:

 

.

(3.11)

 

Каждое уравнение представляет собой сумму перемещений по на­правлению i-й дополнительной связи от внешней нагрузки и реак­ций в дополнительных связях. Общее число уравнений равно числу определяемых реакций. Перемещения от реакций в дополнительных связях, из-за того, что значения этих реакций до решения уравнений (3.11) неизвестны, представляют в виде произведений d_{i j} X_j , где d_{i j} – перемещения по направлению реакции X_i от единичного усилия, на­правление и место приложения которого совпадают с направлением и местом приложения реакции X_j. Свободные члены уравнений есть перемещение по направлению реакции X_i от действия заданной на­грузки.

Система уравнений (3.11) записывается в соответствии со сле­дующими правилами (канонами, поэтому и называется канонической). В каждом уравнении все члены его имеют одинаковый первый ин­декс и располагаются в порядке возрастания второго индекса у коэф­фициентов d_{i j}, последним записывается свободный член . Уравне­ния в системе располагаются в порядке возрастания первого индекса членов уравнений.

Для системы, один раз статически неопределимой, записывается одно уравнение, которое имеет вид

 

.

 

Для системы, два раза статически неопределимой, уравнения имеют вид

 

.

 

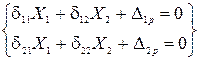Вычисление коэффициентов при неизвестных и свободных чле­нов канонических уравнений.Поскольку коэффициенты d_{i j} и свободные члены есть пере­мещения по направлению неизвестных сил, то для их вычисления можно применять любые методы вычисления перемещений, однако чаще всего применяется метод Мора.

При использовании этого метода на прямолинейных участках для вычисления интегралов Мора, как правило, применяют способ Верещагина. Для этого строят грузовые и единичные эпюры. Сначала основную систему нагружают только заданной на­грузкой. Для полученной таким образом расчетной схемы строят эпюры внутренних силовых факторов (грузовые эпюры). Эти эпюры обозначают M_{x p} , N_p и т.д. Затем ОС нагружают только одним без­размерным единичным усилием , вид, направление и точка прило­жения которого соответствуют виду, направлению и точке приложе­ния неизвестного усилия X₁. Для этой расчетной схемы строят эпюры внут­ренних силовых факторов, которые обозначают M_{x 1} , N₁ и т.д. Затем аналогичным образом поочередно строят эпюры от действия единич­ных усилий, соответствующих остальным неизвестным силам (X₂ , X₃ и т.д.), которые обозначают M_{x 2} , N₂ , M_{x 3} , N₃ и т.д. Эпюры внутренних силовых факторов, возникающих от действия единичных силовых факторов, называют «единичными эпюрами». Все эпюры (грузовые и единичные) строят по обычным правилам (с определе­нием и последующим учетом реакций в опорах, записью аналитиче­ских выражений и т.д.).

Для вычисления коэффициентов канонических уравнений пере­множают эпюры с индексами, совпадающими с индексами вычис­ляемого коэффициента. Так, вычисляя свободный член , пе­ремножают грузовые эпюры (с индексами p) на единичные с индек­сами 2. Вычисляя коэффициент d₂₁, перемножают единичные эпюры с индексами 2 на единичные эпюры с индексами 1. При использова­нии формул (3.1а)…(3.4а) или (3.5, 3.7) эпюры с индексами 2 считаются гру­зовыми, а эпюры с индексами 1 – единичными, или наоборот. При вычислении коэффициента d₂₂ эпюры с индексом 2 перемножаются «сами на себя», каждая из этих эпюр считается одновременно как грузовая и как единичная и т.д.

Примечание. Полезно помнить, что коэффициенты при неизвестных, имеющие одинаковые индексы (главные коэффици­енты), например d₁₁, d₂₂ и т.д., всегда положительны, а коэффициенты, имеющие одинаковый набор индексов, равны между собой, например d₁₂=d₂₁, d₂₃=d₃₂ и т.д.

Если статически неопределимая система имеет криволинейные участки, то на них применять способ Верещагина для вычисления ин­тегралов Мора нельзя. На таких участках интегралы Мора вычисляют прямым интегрированием (см. п. 3.2.1).

Решение системы канонических уравнений.После вычисления всех коэффициентов и свободных членов их, если это возможно, сокращают на общие множители и подставляют в исходную систему уравнений.

Затем решают систему уравнений. Для этого могут применяться лю­бые методы решения систем линейных алгебраических уравнений. Для небольших систем уравнений наименее трудоемким является ме­тод Гаусса. Систему из двух уравнений можно решить методом Кра­мера. Из решения системы канонических уравнений определяют ре­акции в дополнительных связях (неизвестные усилия X_i).

Примечание. Если из решения X_i получена со знаком минус, то это означает, что в действительности она направлена в сто­рону, противоположную ее направлению на эквива­лентной системе.

На этом заканчивается собственно раскрытие статической неоп­ределимости. Дальнейший расчет на проч­ность и (или) жесткость ведут для статически определимой системы, нагруженной заданной нагрузкой и найденными реакциями в дополнительных связях. Обычным образом определяют реакции в необходимых связях, строят эпюры, производят необходимые расчеты.

Для выполнения таких расчетов необ­ходимы эпюры внутренних силовых факторов для заданной системы от суммарного действия приложенной нагрузки и реакций в дополни­тельных связях, поэтому построение этих (суммарных) эпюр включают в алгоритм раскрытия статической неопределимости.

Построение суммарных эпюр.Суммарные эпюры можно построить двумя способами.

1 способ (традиционный)

Основную систему нагружают заданной нагрузкой и найден­ными реакциями в дополнительных связях (X_i). Если из решения X_i получена со знаком «минус», то ее изображают в направлении противо­положном, изображенному на эквивалентной системе. Далее тради­ционным способом строят необходимые эпюры.

2 способ (способ сложения эпюр)

Ординаты суммарной эпюры в любом сечении могут быть полу­чены по следующей схеме:

 

,*

(3.12)

 

где M_c , M_p , M_i – ординаты суммарной, грузовой и единичных эпюр соответственно; L – степень статической неопределимости.

Ординаты эпюр M_p и M_i подставляют в формулу (3.12) с учетом знаков. Правило знаков выбирается студентом, например так, как показано на рис. 5. X_i подставляют с теми знаками, с которыми они получены из решения. Для построения суммарных эпюр достаточно вычислить ординаты M_c на границах участков и в экстремальных точках. Полученные ординаты M_c откладывают от базовой линии, ру­ководствуясь принятым правилом знаков. Полученные точки соеди­няют линиями, которыми ограничена эпюра M_p.

 

* Формула введена автором

Проверка правильности раскрытия статической неопреде­лимости.После того как построены суммарные эпюры, появляется воз­можность надежно проверить правильность выполненного реше­ния. Как отмечалось, перемещения точек приложения связей по на­правлению этих связей в заданной статически неопределимой сис­теме при беззазорном соединении равны нулю, при наличии за­зора – величине зазора. Для проверки правильности решения опреде­ляют перемещение в точке приложения одной из связей по направле­нию этой связи (выполняют деформационную проверку). Если оно окажется равным нулю или величине зазора (при наличии зазора), то все действия по раскрытию статической не­определимости выпол­нены правильно. В противном случае в решении имеются ошибки, которые необходимо найти, устранить и вновь выполнить деформа­ционную проверку.

Для выполнения деформационной проверки суммарные эпюры перемножают на единичные, построенные от действия единичного силового фактора, приложенного к основной системе в точке, где от­брошена дополнительная связь по направлению этой связи. Для по­строения единичных эпюр рекомендуется выбирать иную основную систему, чем та, с использованием которой выполнялось решение.