Некоторые пояснения

4.1. Синусоидальное напряжение 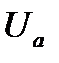при заданной круговой частоте О) полностью определяется своими действующим значением и начальной фазой

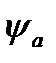
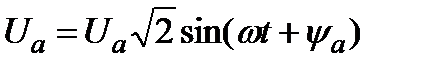(2.1)

Поэтому полную информацию об этом синусоидальном напряжении заданной частоты содержит комплексное напряжение (комплексное действующее значение напряжения):

(2.2)

Аналогично определяются комплексное напряжение

(2.3)

и комплексный ток

2.4)

Иногда комплексные напряжение и ток называют просто комплексами напряжения и тока.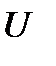

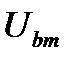В теории цепей часто вместо действующего значения применяют амплитудное значение синусоидальных величин. Например, и – амплитуды двух напряжений, – амплитуда тока. Соответственно определяются и комплексные амплитуды напряжений и токов:

(2.5)

(2.6)

(2.7)

Будем называть сдвигом фаз 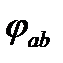между синусоидальными напряжениям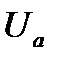и и разность фаз этих напряжений с определенным знаком “+” или “-“:

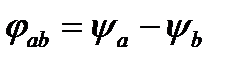(2.8)

Сдвиг фаз в пределах от 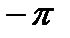до между двумя синусоидальны­ми напряжениями (первое из которых условимся называть "измеряемым'', а второе – "опорным") может быть измерен фазометром. У фазометра, применяемого в нашем лабораторном стенде, может быть измерен сдвиг фаз между двумя синусоидальными потенциалами двух точек схемы – "измеряемым" и "опорным" (или "И" и "О"), причем знак измеренного угла определяется по одному из двух светодиодов: минусу соответствует зажигание левого светодиода, помеченного "I", а плюсу – правого, помеченного "С". Предполагается, что с точкой измеряемого потенциала соединен правый вход "Измер." фазометра, а с точкой опорного потенциала соединен левый вход "Опорн." фазометра.

4.2. Аналогично, сдвигом фаз между напряжением и током

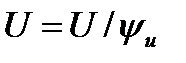(2.9)

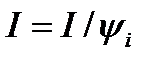(3.1)

будем называть следующий фазовый сдвиг:

(3.2)

Если комплексное напряжение пропорционально комплексному току линейного двухполюсника, то взаимообратные отношения этих комплексов называют комплексным сопротивлением 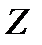и комплексной проводимостью этого двухполюсника:

(3.3)

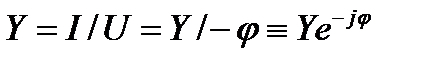(3.4)

Модули комплексного сопротивления и 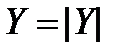комплексной проводимости принято называть соответственно полным сопротивлением и полной проводимостью, а угол называют аргументом комплексного сопротивления.

4.3. Комплексные сопротивление и проводимость иногда представляют в алгебраической форме:

(3.5)

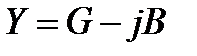(3.6)

где 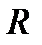– активная составляющая сопротивления, – активная состав­ляющая проводимости, 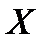– реактивная составляющая сопротивления и – реактивная составляющая проводимости.

Параметры алгебраического представления и полярной формы комплексных сопротивления и проводимости связаны известными соотношениями:

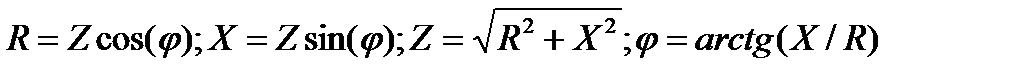(3.7)

(3.8)

4.4. Комплексное сопротивление идеального резистора 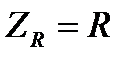является вещественным (его аргумент равен нулю или, при отрицательном сопротивлении резистора, – ±180°).

4.5. Комплексное сопротивление емкости является чисто мнимым числом с аргументом -90° (или +90° , когда емкость является отрицательной. Отрицательные компоненты цепи: сопротивления, емкости и т. п. – это сложные активные устройства, требующие для своего функционирования источников питания. Например, они могут быть реализованы с помощью конвертора отрицательного сопротивления.

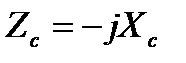(3.9)

Здесь – емкостное сопротивление, которое обратно пропорционально частоте:

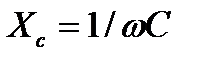(4.1)

 

Не путайте емкостное сопротивление и реактивное сопротивление , которое у емкости обратно по знаку емкостному сопротивлению: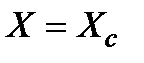

т. е., положительная емкость имеет отрицательное реактивное сопротивление .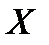

4.6. Емкость обычно реализуется емкостью конденсатора. Реальный конденсатор имеет потери, которые иногда учитываются простейшими последовательной или параллельной схемами замещения (рис. 5, а и б), в которых потери учитываются сопротивлениями потерь или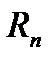

а) б)

Рис 5 – Схемы замещения конденсатора: а) – последовательная, б) – параллельная .

При этом емкость и сопротивление потерь таких схем зависят частоты.

Последнее затрудняет анализ соответствующих цепей в широком диапазоне частот.

Поэтому, были найдены квазиэквивалентные схемы, которые достаточно точно реализуют характеристики реального конденсатора в широком диапазоне частот.

Одна из таких схем (рис. 6) с тремя независящими от частоты параметрам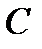и , и обычно достаточно точно передает свойства реальных конденсаторов в диапазоне радиочастот.

Последняя, схема наиболее часто применяется при численном моделировании частотных характеристик электрических цепей с конденсаторами.

В диапазоне сверхвысоких частот в последнюю схему замещения реального конденсатора иногда добавляют индуктивные элементы, позволяющие учесть индуктивность проводников конденсатора.

Рис. 6 – Схема квазиэквивалентная с тремя независящими от частот параметрами .

4.7. При анализе экспериментальной цепи рис. 4 наиболее удобно воспользоваться последовательной схемой замещения конденсатора (рис. 7). Здесь паразитное сопротивление, позволяющее учесть потери в реальном конденсаторе, показано штриховыми линиями.

Рис. 7 – Последовательная схема замещения конденсатора

Пользуясь последней схемой цепи и найденными экспериментальными значениями , не представляет проблем построить векторную диаграмму токов и напряжений экспериментальной цепи. Эта диаграмма построена при дополнительном предложении что начальная фаза тока равна-90 .Поэтому под указанным углом вначале были отложены в некотором масштабе совпадающие по фазе комплексы

Затем построен с учетом найденного фазового сдвига комплекс . И, наконец, с учетом своего фазового сдвига, – вектор, соответствующий комплексу

Проекции из конца последнего вектора на вертикальную и горизонтальную оси определили размер векторов, соответствующих комплексам 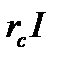и -

 

После расчета по построенной диаграмме значений величин и 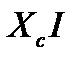подсчета и , может быть уточнено экспериментальное значение емкости конденсатора:

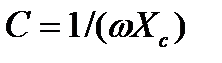, (4.2)

Контрольные вопросы к лабораторной работе.

1. Что такое емкостное сопротивление и как оно связано с реактивным и комплексным сопротивлениями емкости?

2. Как зависит реактивное сопротивление емкости от частоты?

3. Нарисуйте треугольник сопротивлений последовательной цепи.

4. Как определяется сдвиг фаз между двумя гармоническими напряжениями?

5. Как определяется сдвиг фаз между гармоническими напряжением и током?

6. Чему равны активная, реактивная, полная и комплексная мощности в идеальной емкости?

7. Чему равны активная, реактивная, полная и комплексная мощности в резисторе?

8. Чему равны активная, реактивная , полная и комплексная мощности в последовательной цепи?