Вторая квадратичная форма поверхности
ВНЕШНЯЯ ГЕОМЕТРИЯ ПОВЕРХНОСТЕЙ
Пусть F – регулярная поверхность класса С2 и 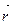 =
=  - ее векторная параметризация, заданная на Q.
- ее векторная параметризация, заданная на Q.
Определение 1. Второй квадратичной формой поверхности F называется скалярное произведение
II = ( 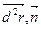 ),
),
где  - нормаль к поверхности F, а
- нормаль к поверхности F, а  - второй дифференциал вектор-функции
- второй дифференциал вектор-функции  . Так как
. Так как
 =
= 
 ) =
) =  =
= 
то
II =  .
.
Введем для коэффициентов второй квадратичной формы следующие обозначения:
L =  , M =
, M =  , N =
, N = 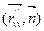 . (1)
. (1)
Тогда
II =  . (2)
. (2)
Поскольку  =
=  =
=  , то имеют место следующие формулы для вычисления коэффициентов второй квадратичной формы:
, то имеют место следующие формулы для вычисления коэффициентов второй квадратичной формы:
L =  M =
M =  N =
N =  (3)
(3)
Пусть поверхность F задана явным уравнением  класса С2. В этом случае векторная параметризация поверхности F имеет вид:
класса С2. В этом случае векторная параметризация поверхности F имеет вид:
 .
.
Ранее мы нашли коэффициенты первой квадратичной формы
Е = 1 +  , F =
, F =  ×
×  , G = 1 +
, G = 1 +  .
.
Найдем производные и коэффициенты второй квадратичной формы:

 ,
,  ,
,  ,
,  ,
, 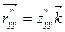 .
.
EG - F2 = (1 +  )×(1 +
)×(1 +  ) –
) –  2 ×
2 ×  2 = 1 +
2 = 1 +  +
+  .
.
(  ) =
) =  =
=  , L =
, L = 
( 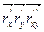 ) =
) =  =
=  , M =
, M = 
(  ) =
) =  =
=  , N =
, N =  .
.
Пример 1. Найти вторую квадратичную форму псевдосферы
 где 0< u < p, 0 £ v < 2p,
где 0< u < p, 0 £ v < 2p,  > 0.
> 0.
Решение. Для нахождения коэффициентов второй квадратичной формы поверхности необходимо найти первые и вторые частные производные вектор-функции поверхности, а также коэффициенты первой квадратичной формы.


 ,
,
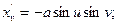

 .
.
Находим коэффициенты первой квадратичной формы поверхности:
E = 
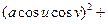
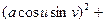
 = =
= = 
 .
.
F =  = 0.
= 0.
G =  =
= 
 =
=  .
.
E G – F2 = ( 
 )
)  = =
= =  =
= 

 .
.
Находим вторые частные производные:
 ,
,
 ,
,
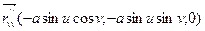 .
.
Ранее мы получили формулы для вычисления коэффициентов второй квадратичной формы:
L =  M =
M =  N =
N =  .
.
( 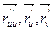 ) =
) =  =
=  (
(  −
−
− 
 (− (
(− (  ) =
) =
= −  +
+  = −
= −  .
.
L =  = −
= −  :
:  = −
= −  .
.
L = −  .
.
(  ) =
) =  =
=
= − 
 (−
(−  +
+  ) = 0.
) = 0.
М =  = 0.
= 0.
(  ) =
) =  =
=
= - 
 (-
(-  -
-  ) =
) = 
 ×
×  =
=
=  .
.
N =  =
=  :
:  =
=  .
.
Ответ: -  du2 +
du2 +  dv2.
dv2.