Екстремум функції
Означення 4.6. Точка  називається точкою максимуму функції
називається точкою максимуму функції  , якщо існує деякий окіл точки
, якщо існує деякий окіл точки  , для точок якого, відмінних від
, для точок якого, відмінних від  , виконується нерівність:
, виконується нерівність:  .
.
Точка  називається точкою мінімуму функції
називається точкою мінімуму функції  , якщо існує деякий окіл точки
, якщо існує деякий окіл точки  , для точок якого, відмінних від
, для точок якого, відмінних від  , виконується нерівність:
, виконується нерівність:  .
.
Означення 4.7. Точками екстремуму функції називаються її точки максимуму та мінімуму.



|
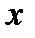
|
 
|
 
|

|
На рисунку в точках  функція набуває максимуму, точках
функція набуває максимуму, точках  функція набуває мінімуму. Точка
функція набуває мінімуму. Точка  - точка перегину.
- точка перегину.
З означення витікає, що точки максимуму та мінімуму є внутрішніми точками області визначення функції та ці поняття є локальними.
Означення 4.8. Критичними точками першого порядку функції називаються точки області визначеності, у яких похідна першого порядку дорівнює нулю, або не існує.
Критичні точки, у яких похідна дорівнює нулю, називають стаціонарними.
Теорема 4.9. (Теорема Ферма, необхідна умова екстремуму). Якщо точка  - точка екстремуму, то вона є критичною точкою першого порядку.
- точка екстремуму, то вона є критичною точкою першого порядку.
Вище було дано означення монотонності функцій, за яким одна з нерівностей  повинна була виконуватись
повинна була виконуватись  . Зараз нам необхідне локальне поняття монотонності.
. Зараз нам необхідне локальне поняття монотонності.
Означення 4.9. Функція називається зростаючою в точці  , якщо існує деякий окіл точки
, якщо існує деякий окіл точки  , у якому вона є зростаючою.
, у якому вона є зростаючою.
Функція називається спадною в точці  , якщо існує деякій окіл точки
, якщо існує деякій окіл точки  , у якому вона є спадною.
, у якому вона є спадною.
Теорема 4.10. Для того, щоб функція, яка має диференціал у точці  , була зростаючою (спадною) в цій точці, необхідно і достатньо, щоб її похідна у
, була зростаючою (спадною) в цій точці, необхідно і достатньо, щоб її похідна у  була додатною (від’ємною).
була додатною (від’ємною).
Достатні умови екстремуму
Теорема 4.11. Якщо  – критична точка першого порядку, і зліва та справа від неї характер монотонності різний, то
– критична точка першого порядку, і зліва та справа від неї характер монотонності різний, то  – точка екстремуму, причому, якщо зліва функція зростає, а справа – спадає, то це точка максимуму, якщо зліва спадає, а справа зростає, то це точка мінімуму.
– точка екстремуму, причому, якщо зліва функція зростає, а справа – спадає, то це точка максимуму, якщо зліва спадає, а справа зростає, то це точка мінімуму.
Теорема 4.12. Якщо  – критична точка першого порядку та існує похідна першого порядку в деякому околі цієї точки, крім, можливо, самої точки, і зліва похідна додатна, а справа – від’ємна, то це точка максимуму, а якщо зліва від’ємна, а справа - додатна, то це точка мінімуму.
– критична точка першого порядку та існує похідна першого порядку в деякому околі цієї точки, крім, можливо, самої точки, і зліва похідна додатна, а справа – від’ємна, то це точка максимуму, а якщо зліва від’ємна, а справа - додатна, то це точка мінімуму.
Теорема 4.13. Якщо  – критична точка першого порядку та в цій точці існує похідна другого порядку, яка від’ємна (
– критична точка першого порядку та в цій точці існує похідна другого порядку, яка від’ємна (  ), то це точка максимуму, а якщо друга похідна додатна (
), то це точка максимуму, а якщо друга похідна додатна (  ), то це точка мінімуму.
), то це точка мінімуму.
Зауваження. Теорема 4.11 ніяких обмежень на функцію не накладає, умова теореми 4.12 потребує, щоб функція мала першу похідну в деякому околі критичної точки, теорема 4.13 потребує існування похідної другого порядку, що, у свою чергу, обумовлює існування першої похідної в деякому околі критичної точки, зокрема, існування похідної в критичній точці, отже, це повинна бути стаціонарна критична точка.
За властивістю неперервних функцій, функція визначена на відрізку  і неперервна на інтервалі
і неперервна на інтервалі  набуває на цьому відрізку своїх найбільшого та найменшого значень. Будемо позначати їх так:
набуває на цьому відрізку своїх найбільшого та найменшого значень. Будемо позначати їх так:
 та
та  .
.
Для знаходження найбільших та найменших значень функції на відрізку знаходять екстремуми функції та обчислюють значення функції в точках екстремуму та в межевих точках, які також є критичними. Серед знайдених значень відбирають найбільше та найменше.
Таке дослідження зручно проводити з використанням таблиці. У першому рядку виписується область визначення, розбита критичними точками першого порядку на інтервали монотонності. У другому – записуються знак похідної на інтервалах монотонності та відмічають, якими є критичні точки: стаціонарні, чи перша похідна не існує. У третьому рядку відображають, зростає чи спадає функція на інтервалах монотонності, а також записують значення функції в критичних точках. Побудову таблиці розглянемо на прикладі.
Знайти точки екстремуму та найбільше і найменше значення функції  на відрізку
на відрізку  .
.
Критичні точки першого порядку, де похідна не існує:  . Знайдемо похідну:
. Знайдемо похідну:  . Ця похідна не існує при
. Ця похідна не існує при  , але ця точка не належить області визначення функції
, але ця точка не належить області визначення функції  . Похідна дорівнює нулю при
. Похідна дорівнює нулю при  але області визначення належить лише
але області визначення належить лише  , отже, стаціонарна критична точка одна.
, отже, стаціонарна критична точка одна.
 при
при 
Критичні точки першого порядку:
 при
при 
Таблиця має вигляд:

| -5 | (-5, -3) | -3 | (-3, -1) | -1 |

| 
|  + +
| - | 
| |

| 
| -2 | 
| ||

|
Критична точка  є точкою максимуму тому, що зліва від неї похідна додатна, а справа – від’ємна. Одночасно, значення функції в цій точці є найбільшим значенням на даному відрізку
є точкою максимуму тому, що зліва від неї похідна додатна, а справа – від’ємна. Одночасно, значення функції в цій точці є найбільшим значенням на даному відрізку  . Найменше значення функції можна знайти, порівнявши
. Найменше значення функції можна знайти, порівнявши  та
та  . Оскільки
. Оскільки  , то
, то  .
.
Означення 4.10. Графік функції називається опуклим на інтервалі, якщо на ньому графік знаходиться під будь-якою дотичною на даному інтервалі.
Графік функції називається угнутим на інтервалі, якщо на ньому графік знаходиться над будь-якою дотичною на даному інтервалі.

|
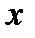
|

|

|

|
Графік опуклої функції

|
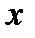
|

|

|

|
Графік угнутої функції
Теорема 4.14. (Достатня умова опуклості (угнутості)). Якщо на деякому інтервалі функція має похідну другого порядку і  , то на цьому інтервалі її графік є опуклим, а якщо
, то на цьому інтервалі її графік є опуклим, а якщо  , то графік є угнутим.
, то графік є угнутим.
Означення 4.11. Точки, у яких відбувається перехід від опуклості до угнутості або навпаки, називаються точками перегину.
За достатньою умовою екстремуму (теореми 4.11, 4.12 та 4.13), якщо характер монотонності функції не змінюється при переході через критичну точку, то екстремуму немає. Це буде точка перегину.
Приклади. 1) Розглянемо функцію  . Її похідна
. Її похідна  в точці
в точці  дорівнює нулю, але і зліва, і справа похідна додатна. Отже, критична точка не є точкою екстремуму.
дорівнює нулю, але і зліва, і справа похідна додатна. Отже, критична точка не є точкою екстремуму.
2) Розглянемо функцію  . Її похідна
. Її похідна  у точці
у точці  не існує, це критична точка першого порядку. Зліва та справа від неї знаки похідної однакові, отже, це точка перегину.
не існує, це критична точка першого порядку. Зліва та справа від неї знаки похідної однакові, отже, це точка перегину.
Теорема 4.15. (Необхідна умова точки перегину). Якщо точка є точкою перегину функції, то похідна другого порядку в ній дорівнює нулю, або не існує, тобто вона є критичною точкою другого порядку.
return false">ссылка скрыта
Через точку перегину можна провести дотичну до графіка функції, причому можливі варіанти: дотична не перпендикулярна до вісі абсцис, або перпендикулярна.
У випадку перпендикулярності, перша похідна не існує, це точка критична першого порядку.
У протилежному випадку в цій точці існує перша похідна, і, якщо вона дорівнює нулю, то це стаціонарна, а тому критична точка першого порядку, якщо перша похідна не дорівнює нулю, то ця точка не є критичною першого порядку.
Означення 4.11. Асимптотою графіка функції називається пряма лінія, до якої необмежено наближаються точки графіка функції при необмеженому віддалені від початку координат.
На відмінну від асимптот гіперболи, графік функції може перетинати асимптоту.
Розрізняють вертикальні та невертикальні асимптоти.
Вертикальні асимптоти, як це випливає із назви, мають рівняння:  , причому
, причому  - точка неусувного розриву функції
- точка неусувного розриву функції  другого роду.
другого роду.
Невертикальні асимптоти мають рівняння прямих з кутовим коефіцієнтом:
 ,
,
де  ,
,  ,
,
за умовою, що вони обидві існують при  або при
або при  .
.
Дослідження точок екстремуму та точок перегину, інтервалів монотонності, опуклості та угнутості, поведінка при  , наявність асимптот дозволяють побудувати ескіз графіка функції.
, наявність асимптот дозволяють побудувати ескіз графіка функції.
4.3. Етапи повного дослідження функції
1. Область визначення функції.
2. Точки перетину графіка з вісями координат.
3. Парність або непарність.
4. Періодичність.
5. Неперервність та точки розриву.
6. Похідна першого порядку та критичні точки першого порядку.
7. Інтервали монотонності.
8. Похідна другого порядку та критичні точки другого порядку.
9. Інтервали опуклості та угнутості графіка функції.
10. Екстремуми функції та точки перегину графіка.
11. Асимптоти графіка функції.
12. Найбільше та найменше значення функції.
13. Множина значень функції.
Приклад. Дослідити функцію  і побудувати її графік.
і побудувати її графік.
1. Область визначення – всі дійсні числа,  .
.
2. Точка перетину з віссю ординат,  :
:  , графік проходить через початок координат. Точки перетину з віссю абсцис,
, графік проходить через початок координат. Точки перетину з віссю абсцис,  , визначає рівняння:
, визначає рівняння:  , яке має один корінь,
, яке має один корінь,  .
.
3. Область визначення симетрична відносно початку координат, можна перевірити парність. Оскільки:  , то функція непарна, і її графік симетричний відносно початку координат.
, то функція непарна, і її графік симетричний відносно початку координат.
4. Функція неперіодична.
5. Функція є добутком двох елементарних, а тому неперервна.
6. Похідна першого порядку:  . Вона дорівнює нулю при
. Вона дорівнює нулю при  . Точок, де перша похідна не існує, немає.
. Точок, де перша похідна не існує, немає.
 - немає
- немає
Критичні точки першого порядку:
 при
при 
7. Монотонність за знаками похідної наведені в таблиці.
8. Похідна другого порядку:
 .
.
Вона дорівнює 0 при  . Точок, де друга похідна не існує, немає.
. Точок, де друга похідна не існує, немає.
 - немає
- немає
Критичні точки другого порядку:
 при
при 
9. Опуклість та угнутість графіка за знаками другої похідної наведено в таблиці.
10. Екстремуми функції та точки перегину графіка наведено в таблиці.
Таблиця має вигляд:

| 
| 
| 
| -1 | 
| 
| 
| 
| 
| ||

| - | 
| - | + | + | - | 
| - | |||

| - | + | + | + | - | - | - | + | |||

| 
| 
| 
| 
| |||||||
| пер. | 
| пер. | 
| пер. |
11. Перевіримо, чи є асимптоти у графіка. Оскільки немає точок неусувного розриву другого роду, то вертикальних асимптот нема. Знайдемо границі:  та
та 
Оскільки ці границі існують при  та при
та при  , то
, то  - вісь абсцис є горизонтальною асимптотою як при
- вісь абсцис є горизонтальною асимптотою як при  , так і при
, так і при  .
.
Ескіз графіка має вигляд:

|
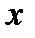
|

|

|

|

|

|
12. Як видно з рисунка, значення функції лежать у проміжку між найменшим та найбільшим її значенням, отже, множина значень  .
.
Завдання для самоперевірки
1. Знайти найбільше та найменше значення функцій на заданих проміжках:
1)  ; 2)
; 2)  ;
;
3)  ; 4)
; 4) 
2. Провести повне дослідження функцій та побудувати їх графіки:
1) 
2. Провести повне дослідження функцій та побудувати їх графіки:
1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  ; 5)
; 5)  .
.
Рекомендована література
1. Лихолетов И.И. Высшая математика, теория вероятностей и математическая статистика - Минск: «Вышєйш. Школа», 1976.
2. Кудрявцев В.А., Демидович Б.П. Краткий курс высшей математики: М., «Наука», 1975.
3. Шкіль М.І. Математичний аналіз: К.: Вища школа, 1994.
4. Бобков Н.Н. Курс математического анализа для студентов экономических специальностей – М., «МАКС Пресс», 2007.
З М І С Т
Передмова 3
3. Вступ до аналізу 4
3.1. Числові послідовності 7
3.2. Границя функції 16
3.3. Неперервність функції 19
3.4. Розкриття невизначеностей 24
3.5. Точки розриву функції 28
4. Диференціальне числення 34
4.1. Диференціал функції 44
4.2. Екстремум функції 45
4.3. Етапи повного дослідження функції 50
Рекомендована література 53