Тема. Метод подбора частного решения неоднородного ЛДУ (2.1) с постоянными коэффициентами и правой частью специального вида.
Лекция 3.
Повторение. Найдём общее решение однородного ЛДУ с постоянными коэффициентами
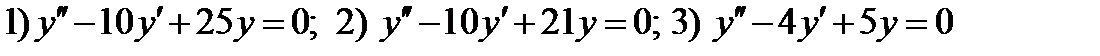 .
.
Решаем первый пример  Выписываем для данного однородного ЛДУ характеристическое уравнение
Выписываем для данного однородного ЛДУ характеристическое уравнение
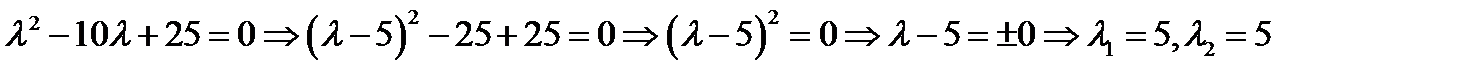
Отсюда (по теореме 2.5 ) определяем
ФСР: 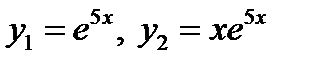
Общее решение :  .
.
Решаем второй пример 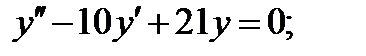 Выписываем для данного однородного ЛДУ характеристическое уравнение
Выписываем для данного однородного ЛДУ характеристическое уравнение
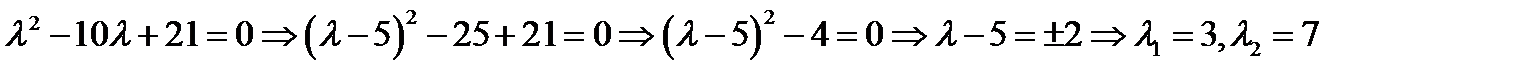
Отсюда( по теореме 2.5 )определяем
ФСР: 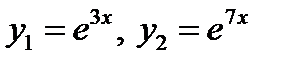
Общее решение :  .
.
Решаем третий пример  . Выписываем для данного однородного ЛДУ характеристическое уравнение
. Выписываем для данного однородного ЛДУ характеристическое уравнение
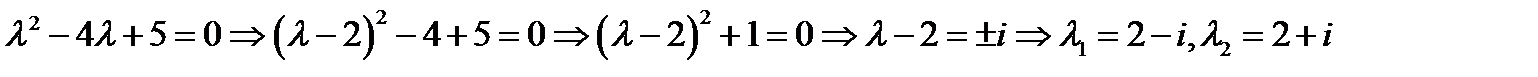
Отсюда (по теореме 2.5 ) определяем
ФСР: 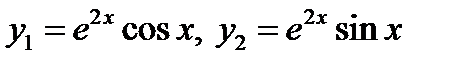 .
.
Общее решение : 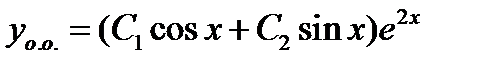 .
.
На прошлой лекции было доказано, что общее решение неоднородного ЛДУ
 (2.1)
(2.1)
даётся формулой
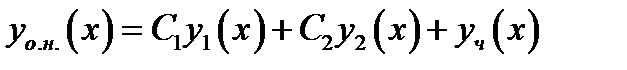 (2.4)
(2.4)
где 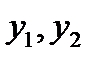 образуют ФСР, а
образуют ФСР, а  некоторое решение неоднородного ЛДУ (2.1)
некоторое решение неоднородного ЛДУ (2.1)
Основной трудностью при вычислении общего решения является нахождение  . Рассмотрим правило нахождения частного решения неоднородного ЛДУ (2.1) с постоянными коэффициентами для функций
. Рассмотрим правило нахождения частного решения неоднородного ЛДУ (2.1) с постоянными коэффициентами для функций 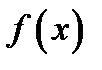 специального вида.
специального вида.