Нелинейная регрессия. Линеаризация переменных

Достаточно часто соотношения между переменными невозможно выразить линейной зависимостью ввиду возникающих больших расхождений между наблюдениями и теоретическими значениями регрессии. В этом случае прибегают к использованию нелинейной регрессии. Регрессия может быть нелинейной относительно независимых переменных, либо относительно оцениваемых параметров.

 

4.1. Нелинейность относительно независимых переменныхПримером регрессий, нелинейных по независимым переменным могут служить полиномы разных степеней, равносторонние гиперболы.

- Полином второй степени у=a₀+a₁x+a₂x²+e .Эта функция, в частности, может быть применена при изучении зависимости между размерами предприятия и издержками на единицу продукции. Сначала увеличение размера предприятия способствует снижению издержек под воздействием эффекта масштаба. Однако, начиная с некоторого момента, рост размеров предприятия увеличивает затраты вследствие усложнения структуры управления и его нерациональной организации. Среди полиномов наиболее часто используются полиномы низших порядков (второго, реже – третьего). Это связано с тем, что

во-первых, чем выше степень полинома, тем больше изгибов имеет кривая, и, следовательно, тем менее однородны исходные данные.

во-вторых, увеличение степени полинома означает включение в модель дополнительной переменной, и, следовательно, возможные сложности при статистической оценке модели.

- Равносторонняя гипербола 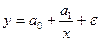. Типичными примерами использования этой функции являются кривая Филлипса, отражающая зависимость прироста заработной платы от безработицы и кривая Энгеля, показывающая зависимость долю расходов на непродовольственные товары от общего уровня доходов.

 

Оценка регрессий, нелинейных относительно независимых переменных достаточно проста. Путем замены переменных они легко сводятся к линейным функциям и оцениваются с помощью метода наименьших квадратов. Для рассмотренных функций ниже приведены примеры таких замен.

Регрессия, нелинейная по независимым переменным	Преобразование
у=a0+a1x+a2x2+e	z=x2 у=a0+a1x+a2z+e
у=a0+a1x+a2x2 + a2x2+e	z=x2 p=x3 у=a0+a1x+a2z + a3p+e
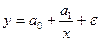
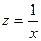	у=a0+a1z +e

 

4.2. Нелинейность относительно параметровпредставляет собой более сложный случай. Эти модели, в свою очередь, могут быть разделены на 2 группы:

ž внутренне линейные модели;

ž внутренне нелинейные модели.

Если нелинейная модель внутренне линейна, то при помощи определенных процедур она может быть сведена к линейной и оценена при помощи метода наименьших квадратов. Напротив, если модель внутренне нелинейна, то к линейной функции ее свести нельзя. В этом случае для проведения эконометрических исследований используются различные итеративные процедуры. Однако намного чаще в практике встречаются внутренне линейные модели. Приведем основные из них:

 

Примеры преобразования внутренне линейных функций.

Внутренне линейная регрессия	Преобразование
Показательная функция y=abxe.	lny=lna+xlnb+lne Y= lny A= lna B=lnb E= lne Y=A+Bx+E
Степенная функция y=axbe	lny=lna+blnx+lne Y= lny A= lna X=lnx E= lne Y=A+bX+E
Экспоненциальная функция y=ea+bxe	lny=a+bx+lne

 

Среди внутренне линейных функций особое место занимает степенная функция, поскольку параметр b в ней интерпретируется как коэффициент эластичности, т.е. показывает, на сколько процентов изменится результат при изменении фактора на 1%.

4.3. Выбор формы модели. Часто этот вопрос решается легко, но в других случаях для принятия обоснованного решения приходится проводить сравнительный анализ нескольких моделей. Для этого требуется выбрать критерии, с помощью которых будет проводиться сравнение. Наиболее часто при сравнении моделей используют следующие критерии:

1. Простота. При прочих равных условиях приоритет отдается модели, имеющей меньшее число объясняющих переменных.

2. Максимальное соответствие, определяемое величиной коэффициента детерминации.

3. Согласованность с теорией. Если уравнение (вид функции, знак при параметре регрессии) не соответствует теоретическим предпосылкам, оно не может быть признано качественным.

4. Прогнозные качества. Полученные при помощи модели значения должны подтверждаться реальностью.