Верификация модели

Прежде чем использовать построенную модель, необходимо оценить ее качество, поскольку:

а) вся информация содержит случайные величины и, если выборка невелика, можно получить искаженные зависимости;

б) возможны ошибки в математической формализации, в этом случае модель также не будет отражать сущность изучаемого явления.

Верификация модели проводится по трем направлениям: соответствие модели эмпирическим данным, качество оценок параметров уравнения регрессии, распределение случайных отклонений.

3.1. Анализ соответствия модели эмпирическим даннымпроводится для того, чтобы определить, в какой степени объясняющая переменная объясняется включенными в модель независимыми переменными. Для этого используется несколько критериев.

F-критерий Фишера основан на анализе квадратов фактических отклонений зависимой переменной от среднего значения. Часть этого отклонения объясняется включенными в модель переменными, а другая - нет:

 

где - рассчитанные значения зависимой переменной по полученному уравнению регрессии;

- среднее значение результативного признака, находимое по эмпирическим данным;

- эмпирические значения результативного признака;

Значимость модели в целом определяют по критерию Фишера F:

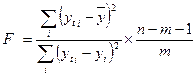, (10)

где m- число объясняющих переменных;

n - объем выборки.

Проверка значимости модели по критерию Фишера основана на тестировании гипотезы о том, что объясненная и остаточная дисперсии в расчете на одну степень свободы различаются незначимо.

По таблице (см. приложение 1) находим значение критерия Фишера F с учетом уровня значимости и числа степеней свободы. Уровень значимости в экономических исследованиях, как правило, выбирается равным 0,05. В этом случае истинное значение параметра регрессии попадает в рассчитанный интервал с вероятностью 0, 95 (p = 1 - a).

Степени свободы рассчитываются следующим образом: k₁=m-1, k₂=n-m.

Найденное в таблице значение сравнивается с табличным. Если рассчитанное по формуле значение больше табличного, то модель считается значимой с вероятностью 1-a. В противном случае модель недостоверна, и необходимо вернуться на предыдущие этапы моделирования.

Для оценки степени соответствия регрессии опытным данным используют также коэффициент детерминации . Он указывает, какая часть общей дисперсии может быть объяснена зависимостью y от x₁,...x_m и изменяется в пределах от 0 до 1:

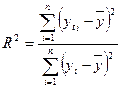. (11)

3.2. Оценка значимости параметров регрессии. Необходимо также оценить, насколько существенно влияют независимые переменные на зависимую. Используя другую выборку для построения такой же модели, мы можем получить как аналогичные результаты, так и совершенно иные. Проверка значимости параметров регрессии состоит в проверке гипотезы о том, что параметры регрессии значимо не отличаются от нуля в генеральной совокупности. Для этого рассчитываются стандартные ошибки оценок параметров регрессии s_b (эта процедура также реализована в статистических пакетах). Чем меньше ошибка параметра, тем выше точность оценивания регрессионной модели и наоборот.

Отношение параметра регрессии к его ошибке сравнивается с критическим значением t_табл критерия Стьюдента. Эта величина берется из таблицы с учетом заданного уровня значимости a и числа степеней свободы. Число степеней свободы f определяется по формуле f=n–m-1, где n - общее количество наблюдений, m - количество объясняющих переменных, a=0,05 (см. приложение 2). Если найденное значение больше табличного, гипотеза о том, что параметр регрессии незначимо отклоняется от нуля, отвергается.

Интерес представляет не только точечная, но и интервальная оценка коэффициентов регрессии, показывающая, в каком интервале изучаемые параметры находятся в генеральной совокупности с заданной вероятностью. В общем случае интервал может быть определен по следующей формуле:

I = (b₁ - t_табл *s_b1; b₁^* + t_табл*s_b1) (12)

При заданном уровне значимости ширина доверительного интервала зависит от объема выборки и от величины стандартной ошибки параметра регрессии. Чем "уже" доверительный интервал, тем точнее построенная оценка генерального параметра. Если в область доверительного интервала попадает число 0, параметр регрессии признается статистически незначимым.

 

3.3. Анализ остатковявляетсяважнейшим направлением статистического анализа модели. Особое внимание при этом должно быть обращено на нормальность их распределения отсутствие гетероскедастичности, и, если анализируются временные модели - на отсутствие автокорреляции.

3.3.1.Нормальность распределения остатков означает, ситуацию, когда наиболее часто встречаются средние по величине отклонения. Отклонения больше и меньше среднего появляются значительно реже:

 

Нормальность распределения остатков может быть проверена, в частности, по критерию Пирсона χ²:

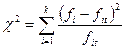, (13)

где

f_i - частоты остатков модели в i-ом интервале;

f_{it –} частоты нормального распределения в i-ом интервале;

k – число интервалов.

Полученное значение сравнивается с табличным χ²_табл при заданном a и числе степеней свободы. Для нормального распределения оно равно k-3. (см. приложение 3).

Если χ²_табл ³ χ², то гипотеза о близости полученного распределения остатков нормальному не отвергается, а имеющиеся отклонения обусловлены случайными колебаниями. Напротив, при χ²_табл < χ расхождение полученного распределения и нормального не может быть объяснено случайными отклонениями и гипотезу о соответствии распределений следует отклонить. Если распределение остатков не является нормальным, использовать полученную модель следует крайне осторожно и по возможности провести дополнительные вычисления.

3.3.2. Автокорреляция остатков.

Автокорреляция остатков обычно свидетельствует об ошибках в спецификации модели, например, о неправильно выбранной форме связи между переменными, о невключении в модель существенного фактора.

 

Пример автокоррелированных остатков:

 

 

Модель с автокорреляцией в остатках нельзя использовать для дальнейшего анализа, так как полученные результаты будут недостоверными. Проверка гипотезы об отсутствии коррелированности остатков основана на расчете статистики Дарбина-Уотсона d:

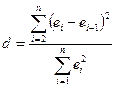, (14)

где

е – разница между наблюдаемым и предсказанным в модели значением зависимой переменной;

Статистика d изменяется в интервале от 0 до 4. При отсутствии автокорреляции в остатках ее значение равно 2. Величина, близкая к 0, свидетельствует о положительной коррелированности остатков, а близкая к 4 – об отрицательной. Выводы о наличии, либо отсутствии автокорреляции делаются на основе специальных статистических таблиц, в которых для заданного числа наблюдений n и уровня a указаны критические значения d_L и d_U . В результате сравнения рассчитанной статистики d с табличными значениями (приложение 4) возможны следующие ситуации:

 

зона неопределенности

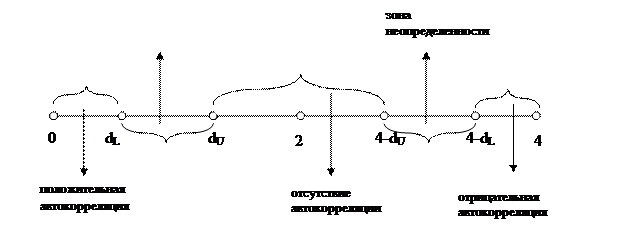
1. d<d_L. Данная ситуация свидетельствует о положительной автокорреляции остатков. Полученную модель использовать нельзя.

2. d_L≤ d≤d_U. Рассчитанная статистика попала в зону неопределенности. Нельзя ни подтвердить, ни отвергнуть гипотезу об отсутствии автокорреляции остатков. Дальнейшие выводы по такой модели должны быть очень осторожными.

3. d_U<d<4-d_U. Гипотеза об отсутствии автокорреляции подтверждается. Модель можно использовать для анализа.

4. 4-d_U≤d≤4-d_L. Рассчитанная статистика попала в зону неопределенности. Нельзя ни подтвердить, ни отвергнуть гипотезу об отсутствии автокорреляции остатков. Дальнейшие выводы по такой модели должны быть очень осторожными.

5. d>4-d_L. Данная ситуация свидетельствует об отрицательной автокорреляции остатков. Полученную модель использовать нельзя.

 

3.3.3. Проблема гетероскедастичности.При построении эконометрических моделей с помощью метода наименьших квадратов (МНК) необходимо проводить анализ дисперсии остатков.

Условие постоянства дисперсий остатков является важнейшей предпосылкой использования МНК. Выполнимость данной предпосылки называется гомоскедастичностью (постоянством дисперсии остатков), а нарушение – гетероскедастичностью.

Требование гомоскедастичности подразумевает, что не должно быть априорной причины, вызывающей в одних наблюдениях заведомо большие остатки, а в других – заведомо малые.

Пример гомоскедастичных остатков:

 

Пример гетероскедастичных остатков:

 

При наличии гетероскедастичности оценки ошибок будут рассчитываться со смещением. Поэтому и все оценки, получаемые на основе t- и F-статистик, будут ненадежными. Их использование может привести к ошибочным данным при проверке качества модели. Как правило, стандартные ошибки коэффициентов регрессии будут занижаться, и, следовательно, статистически значимыми могут быть признаны коэффициенты регрессии, таковыми на самом деле не являющиеся.

Гетероскедастичность достаточно часто встречается в эконометрических исследованиях пространственных выборок. Нередко ее наличие можно предсказать уже на этапе теоретического анализа, предшествующего построению уравнения регрессии.

Предположим, исследуется зависимость между расходами на потребление и величиной душевого дохода. Очевидно, что при росте дохода потребление увеличивается. Но вместе с тем возрастает и дисперсия потребления. У представителей низкодоходных групп доход практически полностью идет на потребление. Но с ростом дохода появляется альтернатива между ростом потребления и сбережениями. Чем выше доход, тем, очевидно, больше простор для распоряжения им. Следовательно, теоретический анализ показывает, что зависимость между расходами на потребление и величиной душевого дохода будет гетероскедастичной. Однако часто выводы о гетероскедастичности делаются на основе анализа уже построенной модели и использования специальных тестов (Голдфелда -Квандта и др.).

Обнаружение гетероскедастичностипроводится с использованием графического и аналитического методов. Так, наличие гетероскедастичности можно определить по полю корреляции:

у

Устранение гетероскедастичности.В МНК все наблюдения имеют одинаковый вес. Но точка, полученная из наблюдений с меньшей дисперсией, более точно определяет направление линии регрессии, чем точка, полученная из наблюдения с большей дисперсией. Поэтому наблюдение с меньшей дисперсией должно иметь больший удельный вес и наоборот, наблюдение с большей дисперсией - меньший удельный вес. В этом случае МНК заменяется на обобщенный метод наименьших квадратов.

Возможным способом является замена переменных на другие, позволяющие избавиться от гетероскедастичности. Например, при анализе расходов на образование в различных странах в в денежном измерении гетероскедастичность будет иметь место, так как страны существенно различаются по численности населения и объему ВВП. В то же время переход к анализу доли ВВП, расходуемой на образование, существенно снизит риск возникновения этой проблемы.