Метод наименьших квадратов

Классификация эконометрических моделей.

1. По содержанию все модели можно разделить на следующие группы:

- аналитические модели, изучающие зависимость значений зависимых переменных от различных факторов;

- прогнозные модели, позволяющие предсказать изменение зависимой переменной во времени.

 

2. По количеству объясняющих переменных все модели делятся на:

- парные (однофакторные) регрессионные модели, в которых используется только одна независимая переменная;

- множественные (многофакторные) регрессионные модели, использующие две и более независимых переменных.

 

3. В зависимости от формы связи между переменными модели могут быть

- линейными;

- нелинейными.

Наибольшее распространение в эконометрическом анализе получили линейные модели ввиду их простоты. Многие нелинейные модели путем несложных преобразований могут быть сведены к линейным.

 

4. По используемым данным:

- пространственные модели, построенные на основе данных, относящихся к одному периоду времени, но к разным объектам;

- временные модели, построенные по данным для одного объекта за разные периоды времени;

- пространственно-временные модели, объединяющие оба вышеприведенных варианта.

 

5. По количеству уравнений (и количеству объясняемых переменных):

  1. одномерные, описывающие поведение одной зависимой переменной;
  2. многомерные, моделирующие поведение двух и более зависимых переменных.

 

6. По характеристикам взаимосвязи зависимой и независимой переменных:

- причинно-следственные модели, где независимая переменная играет роль причины, а зависимая - следствия;

- авторегрессионные модели, где зависимая переменная объясняется через ее же значения в предшествующие периоды времени;

- модели тенденции развития, в которых в качестве независимой переменной выступает время.

Тип модели оказывает большое (а часто и решающее) значение при выборе исследовательских методов, инструментов и конкретных действий.

 

Предположим, у нас имеются серия наблюдений, в каждом из которых зафиксированы значения у и x. Изобразим зависимость между наблюдениями графически:

 

На графике отчетливо видна зависимость между у и x: с ростом значений независимой переменной возрастают и значения зависимой переменной, причем зависимость носит линейный характер, что позволяет перейти к построению линейной регрессионной модели с одной зависимой переменной. Это означает, что необходимо оценить параметры прямой b0 и b1 в уравнении

(5)

Эти параметры должны задавать такую прямую, которая бы наилучшим образом соответствовала точкам, изображенным на графике. Другими словами, отклонения фактических значений от моделируемых должны быть минимальными.

Эту задачу позволяет реализовать метод наименьших квадратов (МНК). С его помощью определяются такие параметры регрессии, которые минимизируют сумму квадратов отклонений фактических и моделируемых значений объясняющей переменной. Если фактические значения обозначить через yi, а рассчитанные по модели - yi, то получим:

(6)

Возведение в квадрат применяется для того, чтобы положительные и отрицательные отклонения не уравновешивали друг друга. Кроме того, при возведении в квадрат большее значение придается бóльшим отклонениям по сравнению (сравните: одно отклонение в три единицы увеличивает значение функции (6) на 32=9 единиц, в то время как три отклонения по одной единице - только на 12+12+12=3).

Графически отклонения между наблюдаемыми и рассчитанными значениями зависимой переменной можно показать на рисунке:

 

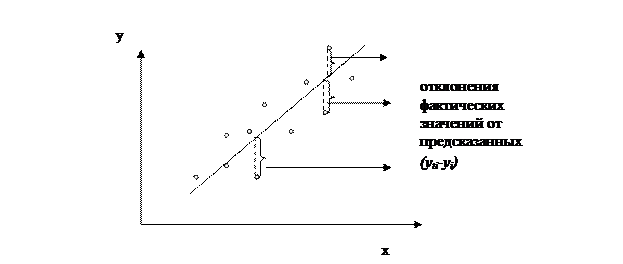
Для случая парной линейной регрессии имеем:

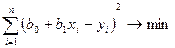(7)

Функция достигает минимума в точке, где первая производная обращается в 0:

 

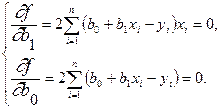(8)

После раскрытия скобок получаем систему линейных уравнений:

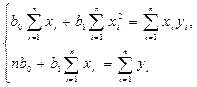(9)

Решая эту систему, находим искомые параметры уравнения регрессии.

В настоящее время процедура расчета параметров регрессии реализована во многих пакетах статистического анализа, в том числе в Excel и Statistica.

Теоретически смысл коэффициента 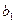заключается в следующем: при увеличении независимой переменной на единицу зависимая переменная изменяется в среднем на величину 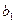. если Что касается коэффициента , то он характеризует среднее значение зависимой переменной, если независимая равна нулю. Однако такая интерпретация возможна не всегда. Например, в модели, рассматривающей зависимость производительности труда от стажа работника, показывает производительность работника с нулевым стажем работы. Если же вместо стажа использовать возраст работников, то подобная интерпретация станет бессмысленной.