ТЕСТ ПО ДИСЦИПЛИНЕ
1. Расположите условия последовательно для исследования экстремума функции:
а)  = 0,
= 0, 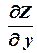 = 0.
= 0.
б) АС - В2 > 0,
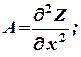
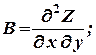
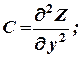
в) АС - В2 = 0;
2. Выберитеадекватные системы стандартных уравнений для функции у = а + а1х1 + а2х2:
а) 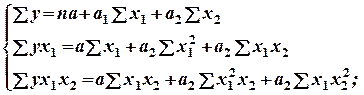
б) 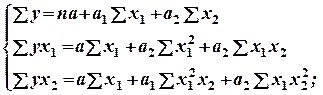
в) 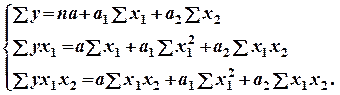
3. Выберите наиболее привлекательные функции для прогнозирования спроса:
а) у = а + bt;
б) у = а + bt + сt2;
в) у = аbt;
г) у = аtb;
д) 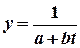 ;
;
е). 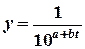
4. Укажите условия, при которых (Н0) отклоняется:
а) Fтабл. < Fфакт.;
б) Fтабл. > Fфакт.;
в) Fфакт. = 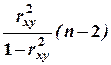 ;
;
г) 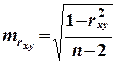 .
.
5. Отметьте нелинейные функции регрессии:
а). у = а + а1х1 + а2х2;
б) 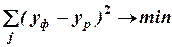 ;
;
в) у = а + bх;
г) 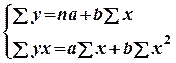
6. Выберите функции автокорреляции:
а) 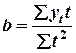 ;
;
б) 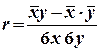 ;
;
в) 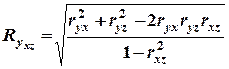
7. Укажите сериальные функции автокорреляции:
а) 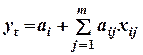 ;
;
б) ∆Z = ƒ (x0 + ∆x1y0 + ∆y) – ƒ(x1y0) < 0;
в) (u1, u2); (u2, u3), …; (um-1, um).
8. Отметьте функции трех точек для прогнозирования:
a) 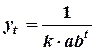 ;
;
б) 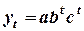 ;
;
в) 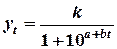 ;
;
г) 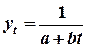 ;
;
д) 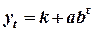 .
.
9. Выберите критерий Дарбина-Уотсона:
а) 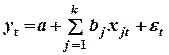 ;
;
б) 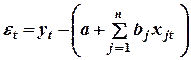 ;
;
в) 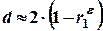 ;
;
г) 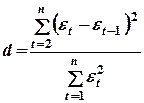 .
.
10. Выберите нестационарные ряды:
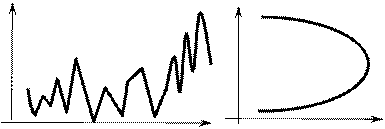 |
а) б)
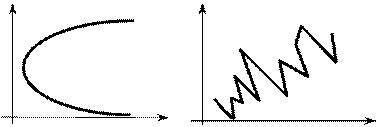
в) г)
 |
д)