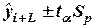Доверительные интервалы прогноза

 

Одна из основных задач, возникающих при прогнозировании, заключается в определении доверительных интервалов прогноза. Интуитивно понятно, что в основе расчета доверительности интервала прогноза должен быть положен измеритель колеблемости ряда. Чем выше эта колеблемость, тем шире интервал для прогноза. Следовательно, вопрос о доверительном интервале прогноза следует начать с рассмотрения измерителя колеблемости. Обычно таким измерителем является среднее квадратическое отклонение:

,

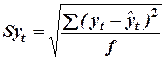где - соответственно фактическое и расчетное значения ряда;

f – число степеней свободы, определяемое в зависимости от числа наблюдений (n) и числа оцениваемых параметров.

f = n – z,

где z – число оцениваемых параметров.

Например, для параболы второй степени f = n – 3, третьей степени f = n – 4 и т.д.

Сумму квадратов отклонений от тренда можно разложить следующим образом:

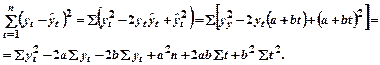
Последнее выражение можно упростить. Допустим, что начало отсчета находится в середине ряда, тогда , а параметры а и b будут равны:

; .

После преобразований получим:

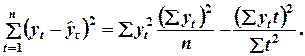
Разность первых двух членов правой стороны равна сумме квадратов отклонений от средней арифметической, т.е. .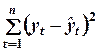

Таким образом,

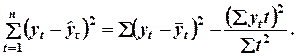
Последнее выражение показывает, что сумма квадратов отклонений от линий тренда меньше, чем от средней арифметической.

Сумма квадратов отклонений от линий тренда, т.е. 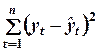и среднее квадратическое отклонение от тренда Sy является основой при определении средней квадратической ошибки параметров.

Прежде чем приступить к определению доверительного интервала прогноза, следовало бы сделать оговорку. Дело в том, что предположение о нормальности распределения отклонений вокруг линии регрессии не может ни утверждаться и не быть проверено при анализе рядов. Дискуссии еще в 30-40-х годах пролили свет на трудности, связанные с этой проблемой. В итоге, принципиальный новый подход так и не был найден. Все предложения так или иначе связаны с определением доверительного интервала на основе оценки среднего квадратического отклонения членов ряда.

Полученные в ходе оценивания параметры не свободны от погрешности. Расчетные значения 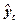несут на себе груз неопределенности, связанной с ошибками в значении параметров.

В общем виде доверительный интервал прогноза определяется как

,

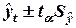где - средняя квадратическая ошибка;

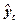- расчетное значение у_t;

- значение t-критерия Стьюдента.

Если t = I + L, то последнее определит значение доверительного интервала на L единиц времени.

Доверительный интервал прогноза должен учитывать не только неопределенность, но возможность отклонения, т.е. диапазон варьирования. Если обозначим среднюю квадратическую ошибку как S_p, тогда доверительный интервал прогноза составит: