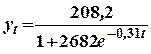Метод трех точек

Предположим, задана логическая кривая -

.

Здесь, также:

;

;

.

Определим параметр а из первого уравнения системы, получим:

Отсюда

,

.

Параметр b найдем из второго уравнения системы, одновременно подставив вместо 10а соответствующее выражение, получим:

.

Отсюда следует, что имеем:

.

Наконец,

.

Подставив в это выражение 10а и 10bn, после соответствующих преобразований, получим:

.

Пример. Предположим, что необходимо провести логическую кривую через три точки. Пусть у₀ = 12,9; у₁ = 62,1; у₂ = 152,7. Интервалы у₀-у₁ и у₁-у₂ равны 6 единицам времени, тогда

 

;

;

.

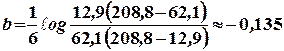Таким образом,

 

 

Аналогичным образом находятся параметры логистической кривой вида:

.

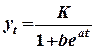Три точки, через которые надо провести кривую можно определить следующим образом:

;

;

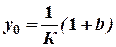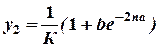
Определим теперь разности d₁, d₂:

;

.

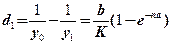Отсюда

.

Итак, .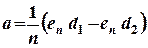

Определим значение выражения. После преобразований получим:

.

Отсюда

.

Следовательно:

.

Наконец, из первого уравнения системы получим:

.

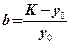Для иллюстрации вернемся к рассмотренному примеру, где у₀ = 12,9; у₁ = 62,1; у₂ = -152,7, n = 6. На основе этих данных получим:

; ;

;

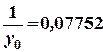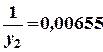d₁ = 0,06142; d₂ = 0,00955;

,

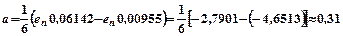
К = 208,2;

.

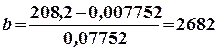Таким образом,

 

Рассмотренный метод оценки параметров весьма прост, однако он очень чувствителен к величине значений у₀, у₁, у₂, которые даже если они получены усредненным путем, могут содержать существенный элемент случайности.