Дробно-рациональные функции

Для оценки технико-экономических показателей также может применяться дробно-рациональные функции. Рассмотренная выше функция является частным случаем дробно-рациональной функции.

Дробно-рациональная функция имеет вид:

Пример 1. Предположим, имеется функция следующего вида:

После преобразования получим:

Из этого следует, что прямые х = 1, х = 2 являются двусторонними (вертикальными) асимптотами графика.

Теперь определим точки максимума и минимума. Предположим, что

или

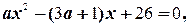
следовательно:

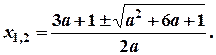
Чтобы прямая у = а пересекла график в двух совпадающих точках, необходимо, чтобы

а² + 6а + 1 = 0

Следовательно:

Это и есть два экстремальных значения функции. Соответствующие им значения аргумента получаем из равенства

Следовательно:

Таким образом, функция имеет максимум, при минимум при График функции представлен на рис. 8.

 

Рис. 8

 

Пример 2. Исследовать и построить график функции:

х² + 1 > 0 при любом х, функция определена на всей числовой оси. Если х = 0, то у = 1, следовательно, график пересекает ось ординат в точке (0,1).

Если х = -1, то у = 0. т.е. график пересекает ось абсцисс в точке -1.

Теперь найдем экстремальные значения функции. Для этого следовало бы найти точки пересечения данной кривой с прямой у = а.

ах² – х – 1 + а = 0

Следовательно,

Далее, путем приравнивания к нулю дискриминанта определим экстремальные значения функции:

1+ 4а - 4а² = 0

.

Итак, ,

Точка есть точка максимума, а точка - минимума.

Для уточнения графика определим еще несколько точек. Если х = 1, то у = 1, если х = 2, то у = 0,6; если х = -2, то График изображен на рис. 9.

 

Рис. 9

 

Пример 3. Исследовать и построить график функции

Область определения функции состоит из двух интервалов: (-∞, 1) и (1, + ∞). Это значит, что график функции состоит из двух ветвей:

.

Найдем точки экстремума. Для этого полагаем, что , следовательно:

Затем, приравнивая дискриминант нулю, получим экстремальные значения функции:

.

Следовательно, .

Таким образом, функция имеет минимум в точке, равной , максимум в точке , равной .

График функции изображен на рис. 10.

 

 

Рис. 10