Условный экстремум
СОДЕРЖАНИЕ
Стр
| ЗАМЕТКИ ПРЕПОДАВАТЕЛЯ (СТАРТОВЫЕ) . | |
| Раздел 1. ОСМЫСЛЕНИЕ МАТЕМАТИЧЕСКОГО АППАРАТА ДЛЯ РЕШЕНИЯ ЭКОНОМИЧЕСКИХ ЗАДАЧ ….………….…. | |
| 1.1. Экстремум функции нескольких переменных ……………………………… | |
| 1.2. Достаточный признак существования экстремума функции двух независимых переменных ……………………………… | |
| 1.3. Условный экстремум ……..…….………. | |
| 1.4. Метод наименьших квадратов …………. | |
| 1.5. Правила составления системы стандартных уравнений ………………… | |
| 1.6. Наиболее привлекательные функции для измерения экономических процессов (спроса, выпуска продукции, ценообразования и других) …………………………. | |
| 1.6.1. Квадратичная функция ………………. | |
| 1.6.2. Биквадратная функция ……………….. | |
| 1.6.3. Кубическая функция …………………. | |
| 1.6.4. Обратнопропорциональная функция ... | |
| 1.6.5. Дробно-линейная функция …………… | |
| 1.6.6. Дробно-рациональная функция ……… | |
| 1.6.7. Степенная функция …………………… | |
| 1.6.7.1. Степенная функция с натуральным показателем ………………………… | |
| 1.6.7.2. Степенная функция с целым отрицательным показателем ………………. | |
| 1.6.7.3. Степенная функция с дробным показателем ………………………………. | |
| 1.6.8. Показательная функция ………………. | |
| 1.6.9. Логарифмическая функция …………... | |
| 1.7. Асимптоты с привлекательными функциями для измерения экономических процессов (показателей) ……………… | |
| 1.8. Некоторые обобщения …………………. | |
| 1.9. Вопросы для самоконтроля ……………. | |
| 1.10. Тренировочные задачи ………………... | |
| 1.11. Тест к разделу 1 ……………………….. | |
| Раздел 2. ЭКОНОМЕТРИЧЕСКИЕ МОДЕЛИ …. | |
| 2.1. Измеряющие (регресионные) модели и корреляция ……………………………… | |
| 2.1.1. Частная корреляция …………………... | |
| 2.2. Имитирование (интерпретация) регрес-сионных моделей …………..…………… | |
| 2.3. Эконометрические модели спроса …….. | |
| 2.4. Эконометрические модели ценообразо-вания …………………………………….. | |
| 2.5. Оценка уравнения регрессии и корреляции ………………………………………. | |
| 2.6. Вопросы для самоконтроля …………….. | |
| 2.7. Тренировочные задачи …………………. | |
| 2.8. Тест к разделу 2 …………………………. | |
| Раздел 3. ЭКОНОМЕТРИЧЕСКИЕ МОДЕЛИ ПРОГНОЗИРОВАНИЯ ………………… | |
| 3.1. Стационарные и нестационарные ряды .. | |
| 3.2. Авторегрессия, автокорреляция ……….. | |
| 3.3. Модели прогнозирования ………………. | |
| 3.4. Экспоненты ……………………………… | |
| 3.5. Кривая Гомперца и логическая кривая ... | |
| 3.6. Гомоскедастичность, гетероскедастич-ность остатков ………………………….. | |
| 3.7. Автокорреляция в остатках, критерий Дарбина-Уотсона ………………………. | |
| 3.8. Упрощенное оценпвание параметров модифицированные экспоненты кривой Гомперца и логической кривой ……….. | |
| 3.8.1. Метод трех сумм ……………………… | |
| 3.8.2. Метод трех точек ……………………... | |
| 3.9. Графическая интерпретация кривых роста …………………………………….. | |
| 3.10. Доверительные интервалы прогноза …. | |
| 3.10.1. Доверительные интервралы прогноза для линейного тренда ……………….. | |
| 3.10.2. Доверительные интервалы полиномов невысоких степеней ……. | |
| 3.11. Критерии точности и надежности прогнозов ………………………………. | |
| 3.12. Вопросы для самоконтроля …………... | |
| 3.13. Тренировочные задачи ……………….. | |
| 3.14. Тест к разделу 3 …………………….…. | |
| Раздел 4. ПРОГРАММНЫЕ ПРОДУКТЫ ……… | |
| 4.1. ПРА-1 и другие ……………………….… | |
| 4.2. Тренировочные задачи ………………… | |
| ТЕСТ ПО ДИСЦИПЛИНЕ ………..………………. | |
| ЗАКЛЮЧЕНИЕ …………………………………..… | |
| ЛИТЕРАТУРА ……………………………………… |
ЗАМЕТКИ ПРЕПОДАВАТЕЛЯ
(СТАРТОВЫЕ)
Что такое эконометрика? Можно ли сказать, что эконометрика - это наука об экономических измерениях, как подсказывает ее название? Можно, но все же возникает вопрос, какой смысл вкладывать в термин "эконометрическое измерение". Это аналогично тому, как если бы определить математику как науку о числах. Поэтому, не пытаясь развивать эту проблему, приведем высказывания признанных авторитетов в экономике и эконометрике.
"Эконометрика позволяет проводить количественный анализ реальных экономических явлений, основываясь на современном развитии теории и наблюдениях" (Самуэльсон).
"Основная задача эконометрики - наполнить эмпирическим содержанием априорные экономические рассуждения" (Клейн.)
"Цель эконометрики - эмпирический вывод экономических законов. Эконометрика дополняет теорию, используя реальные данные для проверки и уточнения постулируемых отношений" (Моленво).
Эконометрика предполагает изучение, измерение, измерение количественных характеристик отдельных экономических показателей, исследование зависимостей между показателями.
Эконометрика формирует модели спроса, предложения, ценообразование; модели экономического развития, равновесия. На основе эконометрических методов делаются прогнозы, обосновывают рекомендации по экономической политике.
На основе эконометрических методов выявляются приоритетные направления деятельности фирм, предприятий и т.д., обосновываются какие товары надо производить в каком количестве, какого качества и, на какой рынок следует ориентироваться и т.д.
Эконометрика как наука расположена где-то между экономикой, статистикой и математикой. Один из ответов на вопрос, что такое эконометрика, действительно может звучать так: это наука, связанная с эмпирическим выводом экономических законов. То есть мы используем данные или "наблюдения" для того, чтобы получить количественные зависимости для экономических соотношений. Данные, как правило, не являются экспериментальными, так как в экономике мы не можем проводить эксперименты.
Хотя отмеченное - это только часть работы эконометриста. Он также формулирует экономические модели, основываясь на экономической теории или на эмпирических данных, оценивает неизвестные величины в этих моделях, делает прогнозы и дает рекомендации по экономической политике.
Во всей этой деятельности существенным является использование моделей. Модели должны быть "настолько просты, насколько возможно, но не проще". В большинстве случав экономические законы выражаются в относительно простой математической форме.
Вполне осознанно допускаю, что эта первая редакция не будет лишена недостатков. Все предложения, пожелания благодарно будут учтены к следующему этапу.
Отзывы и предложения прошу направить по адресу: 109803, г.Москва, ул. Земляной вал, 73, МГУ ТУ.
РАЗДЕЛ 1. ОСМЫСЛЕНИЕ
МАТЕМАТИЧЕСКОГО АППАРАТА
ДЛЯ РЕШЕНИЯ ЭКОНОМИЧЕСКИХ ЗАДАЧ
Для предпринимателей, бизнесменов, экономистов, менеджеров, в конкретных обстоятельствах необходимо знать, оценить за счет каких факторов, и в какой степени можно увеличить прибыль предприятия, снизить издержки производства и т.д., т.е. необходимо количественно оценить возможные сценарии развития ситуации. Решение подобных задач, как правило, осуществляется на основе разумного применения теории функционального анализа, теории вероятности и математической статистики.
Цель раздела: осмыслить математический аппарат с практических позиций для решения конкретных экономических задач.
1.1. Экстремум функции нескольких переменных
Практические занятия по курсу: "Эконометрика" начнем с исследования функции ─ на экстремум. Безусловно, вопросы исследования экстремума функции слушатели знают из курса математического анализа. Но, здесь как бы мы повторяем с позиции оценки экономических показателей, в частности прибыли, издержки производства, рентабельности производства или продукции и т.д.
В первую очередь, введем некоторые определения:
Определение 1. Функция Z = ƒ (x, y) имеет максимум в точке М0 (х0, у0), если значение функции в этой точке больше значений ее в точках, достаточно близких к точке М0 (х0, у0), т.е.
ƒ (х0, у0) > ƒ (х0 + Δх, у0 + Δу).
Это означает, что полное прекращение функции Z = ƒ (х, у), вызванное переходом от точки (х0, у0) к соседней точке, будет величиной отрицательной:
ΔZ = ƒ (х0 + Δх, у0 + Δу) - ƒ (х0, у0) < 0. (1)
Определение 2. Функция Z = ƒ (x, y) имеет минимум в точке М0 (х0, у0), если значение функции в этой точке меньше значений ее в точках, достаточно близких к точке М0 (х0, у0), т.е.
ƒ (х0, у0) < ƒ (х0 + Δх, у0 + Δу).
Это означает, что полное прекращение функции Z = ƒ (х, у), будет величиной положительной:
ΔZ = ƒ (х0 + Δх, у0 + Δу) - ƒ (х0, у0) > 0. (2)
Допустим, что функция Z = ƒ (х, у) имеет в точке М0 (х0, у0) максимум или минимум (экстремум). Тогда для функции должно удовлетворяться одно из неравенств (1) или (2) при любых, достаточно малых Δх, Δу.
Предположим, что Δу = 0; тогда функция Z = ƒ (х, у) сделается функцией только одной переменной х. Эта функция по условию имеет экстремум. Таким образом, условия обращения в нуль частных производных функции или несуществование хотя бы одной из них являются необходимыми условиями, но недостаточными условиями экстремума функции.
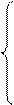Итак, 
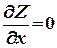
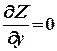. (3)
Условия (3) являются необходимыми для существования экстремума функции. Но может случиться, что эти условия в некоторых обстоятельствах невыполнимы.
1.2. Достаточный признак существования
экстремума функции двух независимых переменных
Продолжаем курс лекций по эконометрике в части математического обеспечения. Напоминаем, что эконометрика в большей степени должна способствовать выявлению вариантных экономических решений с учетом комплексного охвата, как внутренних, так и внешних факторов.
Достаточные условия существования экстремума функции нескольких переменных имеют более сложный вид.
Пусть в точке М0 (х0, у0) частные производные обращаются в нуль, т.е.
, 
.
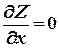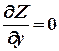Подсчитаем значения частных производных второго порядка функции Z = ƒ (х, у) в этой точке и обозначим их соответственно буквами: А, В, С:
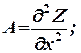
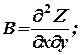
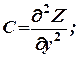
тогда:
1. Если АС - В2 > 0, то функция Z = ƒ (х, у) имеет в точке М0 (х0, у0) экстремум, а именно:
при А < 0 максимум,
при А > 0 минимум.
2. Если АС - В2 < 0, то функция Z = ƒ (х, у) не имеет в точке М0 (х0, у0) экстремума.
3. Если АС - В2 = 0, то вопрос о существовании экстремума функции в точке М0 (х0, у0) остается открытым и требуются дополнительные исследования.
Нередко при отыскании экстремума функции многих переменных аргументы функции связаны между собой одним или несколькими уравнениями, называемыми уравнениями связи. Число таких уравнений, естественно, должно быть меньше числа переменных величин, в противном случае переменные величины могут превратиться (при решении системы) в постоянные величины.
В этом случае, как правило, говорят об условном экстремуме. В отличие от обычного экстремума здесь речь идет о точках, координаты которых удовлетворяют уравнению связи. Предположим, что задана функция у = ƒ (х, у) и уравнение связи у = φ (х), представляемое линией L на плоскости 0ХУ. При этом задача отыскания условий экстремума функции Z = ƒ (х, у) будет состоять в том, чтобы на линии L найти такие точки, в которых значения функции будут наибольшими или наименьшими по сравнению со значениями ее в достаточно близких точках линии L.
Рассмотрим задачу на отыскание условий экстремума функции для того случая, когда задана функция двух переменных Z = ƒ (х, у), а уравнение связи имеет вид φ (х, у) = 0.
Если уравнение связи разрешимо относительно у, т.е. из него можно явно выразить у через х: у = ψ (x), то, делая подстановку в выражение функции Z = ƒ (х, у), получим функцию одной переменной:
Z = ƒ [x, ψ (x)] = F (x).
В случае, когда из уравнения связи не удается выразить одну переменную через другую, пользуются так называемым методом неопределенных множителей Лагранжа. Чтобы найти точки, которые могут быть точками условного экстремума функции Z = ƒ(х, у) при уравнении связи φ(х, у) = 0, нужно образовать вспомогательную функцию (ее часть называют функцией Лагранжа).
Ф (х, у) = ƒ (х, у) + λφ (х, у),
где λ - некоторая постоянная.
Затем, необходимо составить уравнение для отыскания точек экстремума. Очевидно, что таких уравнения должно быть три по числу неизвестных: х, у, λ.
Находим частные производные функции Ф (х, у) и используя необходимые условия существования экстремума функции получим эти три уравнения:
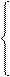ƒ'x (x, y) + λφ'x (x, y) = 0
ƒ'y (x, y) + λφ'y (x, y) = 0
φ (x, y) = 0
Пример 1. Найти экстремум функции
Z = x + y
при условии, что
.
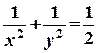Решение:
а). Составляем функцию Лагранжа
Ф (х, у) = х + у + λ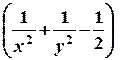 
б). Находим частные производные первого порядка
; 
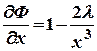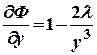
с). Используя необходимые условия существования экстремума функции Ф (х, у) и уравнение связи, получаем систему:
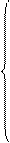
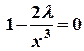
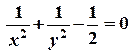
д). Далее решая последнюю систему и используя условия экстремума, получаем две критические точки:
Р2 (-2, -2); Р2 (2, 2).
В первом случае функция имеет значения - 4, а во втором +4. В точке Р2 функция Z имеет максимум, а в точке Р2 - минимум.
Пример 2. Требуется найти экстремум функции
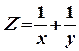
при условиях, что
х + у = 2.
Решение. Также составляем функцию Лагранжа:
Ф (х, у) =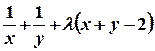
Находим частные производные первого порядка функции Лангранжа:
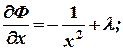
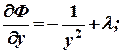
Составляем систему уравнений:
.
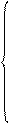
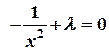
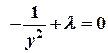х + у - 2 = 0
Можно показать, что в точке (1,1) данная функция Z имеет минимум, равное 2.
Примечание. Данный пример в виду его простоты можно решить и без использования функции Лагранжа.