С автокорреляцией остатков
Линейная модель множественной регрессии
Проверка гомоскедастичности дисперсии по критерию Бартлетта
| Y | Ошибка ei | ei2 | Y | Ошибка ei | ei2 |
| -2,49 | 6,20 | -0,68 | 0,46 | ||
| -1,86 | 3,46 | 5,27 | 27,72 | ||
| 31,93 | 1019,21 | 5,8 | -5,29 | 27,93 | |
| 7,5 | -3,18 | 10,11 | 13,8 | -16,74 | 280,23 |
| -2,17 | 4,71 | 6,2 | 8,94 | 79,87 | |
| -18,38 | 337,64 | 7,9 | -3,57 | 12,74 | |
| 11,5 | -3,45 | 11,90 | 5,4 | 5,18 | 26,79 |
| 5,58 | 31,14 | 7,72 | 59,60 | ||
| 15,8 | -3,11 | 9,67 | 25,5 | -0,85 | 0,72 |
| -8,72 | 76,04 | 7,1 | 4,85 | 23,47 | |
 =167,41
|  =59,69
|
Таблица 4.2
| Переменные | Коэффициент | Стандартная ошибка | Значение t-статистики | Значение критерия Фишера F(2,17) | R2 | |||||
| до | после | до | после | до | после | до | после | до | после | |
| X1 | 1,156 | 1,156 | 0,246 | 0,251 | 4,694 | 4,588 | 24,17 | 20,87 | 0,73 | 0,73 |
| X2 | 15,104 | 15,104 | 3,352 | 4,112 | 4,505 | 3,673 | ||||
| Константа | -17,313 | -17,313 | 6,447 | 5,297 | -2,685 | -3,268 |
Вернемся еще раз к предположению (3.3). Из него, в частности, следует, что ковариации случайной ошибки для разных наблюдений равны нулю. Если к тому же случайные ошибки распределены нормально, то это означает их попарную независимость.
Однако регрессионные модели в экономике часто содержат стохастические зависимости между значениями случайных ошибок – автокорреляцию ошибок. Ее причинами являются: во-первых, влияние некоторых случайных факторов или опущенных в уравнении регрессии важных объясняющих переменных, которое не является однократным, а действует в разные периоды времени; во-вторых, случайный член может содержать составляющую, учитывающую ошибку измерения объясняющей переменной.
Применение к модели с автокорреляцией остатков обыкновенного МНК приведет к следующим последствиям:
1. Выборочные дисперсии полученных оценок коэффициентов будут больше по сравнению с дисперсиями по альтернативным методам оценивания, т.е. оценки коэффициентов будут неэффективны.
2. Стандартные ошибки коэффициентов будут оценены неправильно, чаще всего занижены, иногда настолько, что нет возможности воспользоваться для проверки гипотез соответствующими точными критериями – мы будем чаще отвергать гипотезу о незначимости регрессии, чем это следовало бы делать в действительности.
3. Прогнозы по модели получаются неэффективными.
На практике исследователь в этом случае поставлен перед проблемой тестирования наличия в модели автокорреляции, а также выявления причины автокорреляции при ее обнаружении: или в модели опущена существенная переменная, или структура ошибок зависит от времени. То есть, исследование остатков позволяет судить о правильности модели и ее пригодности для прогнозирования.
Простейшим способом проверки наличия автокорреляции является графическое изображение остатков ei. Возможно построение:
· графика временной последовательности, если остатки получены в разные моменты времени;
· графика зависимости остатков от значений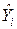 
, полученных по регрессии;
· графиков зависимости остатков от объясняющих переменных.
Если изображение остатков представляет собой горизонтальную полосу, это указывает на отсутствие каких-либо проблем, связанных с моделью. В противном случае в зависимости от вида и типа графика можно получить информацию о: неадекватности модели, ошибочности расчетов, необходимости включения в модель линейного или квадратичного члена от времени; наконец о непостоянстве дисперсии.
Ясно, что ошибки могут коррелировать по-разному, однако без нарушения общности можно рассматривать так называемую сериальную корреляцию (автокорреляцию), когда зависимость между ошибками, отстоящими на некоторое количество шагов s, называемое порядком корреляции (в частности, на один шаг, s=1), остается одинаковой, что хорошо проявляется визуально на графике в системе координат (ei; ei-s). Например, для s=1 на рис. 4.2 показаны отрицательная (слева) и положительная (справа) автокорреляция остатков. В экономических исследованиях чаще всего встречается положительная автокорреляция.
 |  | ||