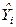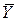Парная регрессия и метод наименьших квадратов

Будем предполагать в рамках модели (2.2) линейную зависимость между двумя переменными Y и X. Т.е. имеем модель парной регрессии в виде:

Y_i =a+bX_i+u_i, i=1,…,n.

а. Eu_i=0, i=1,…,n.

б.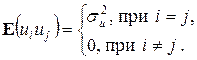

в. X₁, …, X_n – неслучайные величины.

Предположим, что имеется выборка значений Y и X.

Обозначим арифметические средние (выборочные математические ожидания) для переменных X и Y:

.

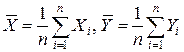Запишем уравнение оцениваемой линии в виде:

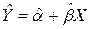, (2.6)

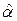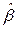где и - оценки неизвестных параметров a и b, а - ордината этой линии.

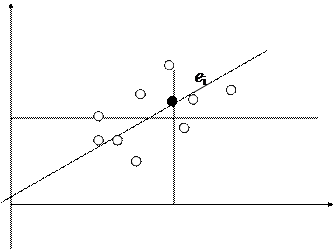
Пусть (X_i, Y_i) одна из пар наблюдений. Тогда отклонение этой точки (см. рис. 2.1) от оцениваемой линии будет равно e_i=Y_i - .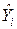

Принцип метода наименьших квадратов (МНК) заключается в выборе таких оценок 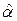и 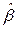, для которых сумма квадратов отклонений для всех точек становится минимальной.

Y

 

 

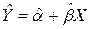
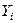
X

 

Рис. 2.1. Иллюстрация принципа МНК

 

Необходимым условием для этого служит обращение в нуль частных производных функционала:

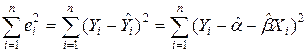
по каждому из параметров. Имеем:

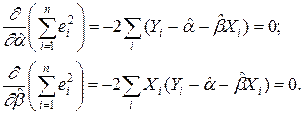
Упростив последние равенства, получим стандартную форму нормальных уравнений, решение которых дает искомые оценки параметров:

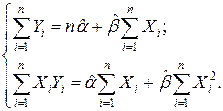(2.7)

Из (2.7) получаем:

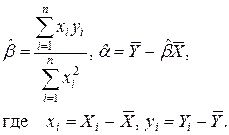(2.8)

Пример. Для иллюстрации вычислений при отыскании зависимости с помощью метода наименьших квадратов рассмотрим пример (табл. 2.1).