Множественная регрессия и корреляция

Лекция 2.

При решении практических задач исследователи сталкиваются с тем, что корреляционные связи не ограничиваются связями меж­ду двумя признаками: результативным у и факторным х. В дейст­вительности результативный признак зависит от нескольких фак­торных. Например, инфляция тесно связана с динамикой потребительских цен, розничным товарооборотом, численностью безработных, объемами экспорта и импорта, курсом доллара, ко­личеством денег в обращении, объемом промышленного производ­ства и другими факторами.

В условиях действия множества факторов показатели парной корреляции оказываются условными и неточными. Количественно оценить влияние различных факторов на результат, определить форму и тесноту связи между результативным признаком у и фак­торными признаками х₁, х₂, ..., x_k можно методами множественной (многофакторной) корреляции.

Многофакторный корреляционно-регрессионный анализ сво­дится к решению следующих задач:

• обосновать взаимосвязи факторов, влияющих на исследуе­мый показатель;

• определить степень влияния каждого фактора на результа­тивный признак путем построения модели-уравнения мно­жественной регрессии, которая позволяет установить, в ка­ком направлении и на какую величину изменится результативный показатель при изменении каждого факто­ра, входящего в модель;

• количественно оценить тесноту связи между результативным признаком и факторами.

Включение в уравнение множественной регрессии того или иного набора факторов связано прежде всего с представлением исследователя о природе взаимосвязи моделируемого показателя с другими экономическими явлениями. Факторы, включаемые во множественную регрессию, должны отвечать следующим требованиям:

1) быть количественно измеримыми;

2) не должны быть коррелированны между собой и тем боле находиться в точной функциональной связи.

Наличие между двумя факторами весьма тесной линейной связи (парный коэффициент корреляции r_хх превышает по абсолютной величи­не 0,7) называется коллинеарностью, а между несколькими факто­рами — мультиколлинеарностью.

Мультиколлинеарность – это нестрогая линейная зависимость между факторными признаками, которая приводит к следующим нежелательным последствиям:

1. Оценки параметров становятся ненадежными, они обнаруживают большие стандартные ошибки, малую значимость, в то же время модель является значимой, т.е. значение множественного коэффициента корреляции завышено;

2. Небольшое изменение исходных данных приводит к существенному изменению оценок параметров модели;

3. Оценки параметров модели имеют неправильные знаки или неоправданно большие значения, что делает модель непригодной для анализа и прогнозирования;

4. Становится невозможным определить изолированное влияние факторов на результативный показатель.

В наибольшей степени ответственным за мультиколлинеарность будет тот признак, который теснее связан с другими факторами модели (он имеет высокие по модулю значения коэффициентов парной линейной корреляции). Поэтому, если факторы явно коллинеарны, то они дублируют друг друга и один из них рекомендуется исключить из регрессии. Предпочтение при этом отдается не фактору, более тесно связанному с результатом, а тому фактору, который при достаточно тесной связи с результатом имеет наименьшую тесноту связи с другими факторами.

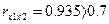Пример. Проверим наличие мультиколлинеарности между факторами х₁ (возраст, лет), х₂ (стаж работы, лет), х₃ (выработка шт./смену), которые могут оказывать влияние на результативный признак - заработная плата. Для этого построим корреляционную матрицу. Из матрицы видно, что между признаками имеется довольно сильная линейная зависимость, т.к. . Вследствие этого требуется устранить один из факторов.

Таблица 1

	y	x1	x2	х3
y
x1	0,853056
x2	0,849877	0,935263
x3	0,778766	0,615448	0,69661

 

Из модели следует исключить фактор х₂, т.к. он теснее связан с третьим фактором, чем фактор х₁: .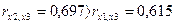

Определившись с набором факторов, исследователи переходят к построению многофакторной эконометрической модели. Математически задача сводится к нахождению аналитического выражения, наилучшим образом описывающего связь факторных признаков с результативным, т.е. к отысканию функции вида:

у = f(x₁, х₂, ..., x_k).

 

Выбрать форму связи довольно сложно. Эта задача на практике основывается на априорном теоретическом анализе изучаемого явления и подборе известных типов математических моделей.

Среди многофакторных регрессионных моделей выделяют ли­нейные (относительно независимых переменных) и нелинейные.

Наиболее простыми для построения, анализа и экономической интерпретации являются многофакторные линейные модели, ко­торые содержат независимые переменные только в первой степени:

 

,

 

где a – свободный член, параметр, представляющий собой среднее значение y при x₁=х₂=…=х_k=0.

b_j – коэффициент регрессии при j-ом факторе (j=1;k). Характеризует среднее изменение признака-результата у в связи с изменением соответствующего фактора х_j на единицу, при условии, что прочие факторы модели не изменяются и фиксированы на средних уровнях;

y_i – значение признака-результата для i–го наблюдения;

x_i – значение j-го фактора для i–го наблюдения;

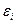- случайная составляющая результативного признака i–го наблюдения.

Если связь между результативным признаком и анализируемы­ми факторами нелинейна, то выбранная для ее описания нелиней­ная многофакторная модель (степенная, показательная и т.д.):

Степенная - ;.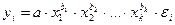

Экспонента – ;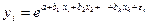

Гипербола – ;

мо­жет быть сведена к линейной путем линеаризации.

Параметры уравнения множественной регрессии, как и парной, рассчитываются методом наименьших квадратов, при этом реша­ется система нормальных уравнений с k +1 неизвестными:

 

 

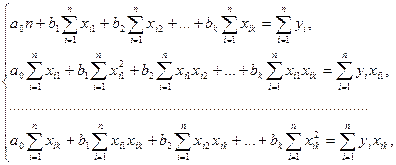
где х_ij — значение j-го факторного признака в i-м наблюдении;

у_i — значение результативного признака в i-м наблюдении.

 

Как правило, прежде чем найти параметры уравнения множест­венной регрессии, определяют и анализируют парные коэффици­енты корреляции:

 

.

 

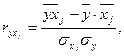
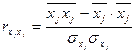При этом систему нормальных уравнений мож­но видоизменить таким образом, чтобы при вычислении параметров регрессии использовать уже найденные парные коэф­фициенты корреляции. Для этого в уравнении регрессии заменяют переменные у, х₁, х₂, ..., x_k переменными t_i, полученными следую­щим образом:

 

 

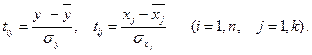
Эта процедура называется стандартизацией переменных. В резуль­тате осуществляется переход от натурального масштаба переменных х_ij к центрированным и нормированным отклонениям t_ij. В стандартизированном масштабе среднее значение признака равно 0, а среднее квадратическое отклонение равно 1, т.е. .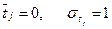

При переходе к стандартизированному масштабу переменных уравнение множественной регрессии принимает вид:

 

,

 

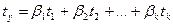где 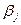(j = 1, k ) — стандартизированные коэффициенты регрессии.

 

-коэффициент характери­зует изменение исследуемого показателя в зависимости от изме­нения одного фактора при постоянном уровне остальных. Иначе, -коэффициент показывает, на какую часть сигмы () изменилось бы значение результата, если бы соответствующий j-фактор изменился на сигму (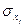), а прочие факторы не измени­лись бы.

Кроме того, -коэффициенты позволяют оценить степень воз­действия факторных признаков на результат. В силу того что все -коэффициенты выражены в одинаковых единицах измерения, при ₂ > ₃ фактор х₂ сильнее влияет на результативный признак, чем фактор х₃.

К уравнению множественной регрессии в стандартизованном масштабе применяется МНК. -коэффициенты определяются из следующей системы уравнений:

 

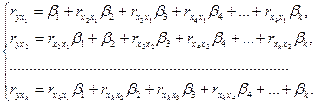
Связь коэффициентов множественной регрессии b_i со стандартизованными коэффициентами описывается соотношением 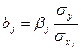. Параметр а определяется как .

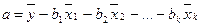В двухфакторном регрессионном анализе найти уравнение регрессии в стандартизированном масштабе 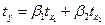можно через формулы:

 

, .

 

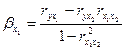На основе линейного уравнения множественной регрессии:

 

 

могут быть найдены частные уравнения регрессии:

 

 

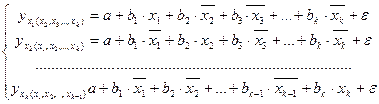
В отличие от парной регрессии частные уравнения регрессии характеризуют изолированное влияние фактора на результат, ибо другие факторы закреплены на неизменном среднем уровне. Это позволяет на основе частных уравнений регрессии определять частные коэффициенты эластичности:

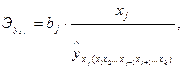
где b_j – коэффициент регрессии при j-ом факторе;

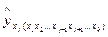‒ частное уравнение регрессии.

 

Для того чтобы оценить сравнительную силу влияния факторов, по каждому фактору рассчитывают средние коэффициенты элас­тичности:

,

 

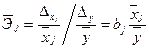где 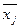— среднее значение j-го факторного признака;

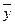— среднее значение результативного признака;

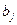— коэффициент регрессии при j-м факторном признаке.

 

Расчет коэффициента эластичности дополняет экономический анализ. Данный коэффициент показывает, на сколько процентов следует ожидать изменения результативного показателя при изме­нении фактора на 1% и неизменном значении других факторов.

Практическая значимость уравнения множественной регрессии оценивается с помощью показателя множественной корреляции и его квадрата – коэффициента детерминации. Показатель множественной корреляции характеризует тесноту связи рассматриваемого набора факторов с исследуемым признаком, или оценивает тесноту совместного влияния на результат.

Независимо от формы связи показатель множественной корреляции может быть найден как индекс множественной корреляции:

 

 

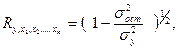
где 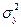— общая дисперсия результативного признака;

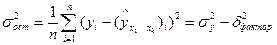— остаточная дисперсия, характеризующая отклонения фактических уровней результативного признака y_i от рассчитанных по уравне­нию множественной регрессии .

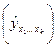При линейной зависимости признаков формула индекса корреляции может быть представлена следующим выражением:

 

 

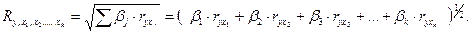
Формула индекса множественной корреляции для линейной регрессии получила название линейного коэффициента множественной корреляции или совокупного коэффициента корреляции.

При линейной форме связи расчет совокупного коэффици­ента корреляции можно также выполнить, используя парные коэффи­циенты корреляции:

 

 

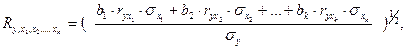
где b₁, b₂, ..., b_k — параметры уравнения множественной регрессии

в натуральном масштабе.

 

Наряду с измерением совместного влияния отобранных факто­ров на результативный признак важно определить воздействие каж­дого фактора при элиминировании его взаимосвязи с остальными (что возможно, когда последние зафиксированы на постоянном уровне). Для решения данной задачи при линейной связи применяют частные коэффициенты корреляции, а для нелинейной - частные индексы детерминации.

В общем виде при наличии k факторов для уравнения:

 

 

коэффициент частной корреляции, измеряющий влияние на у фактора х_k при неизменном уровне других факторов, можно определить по формуле:

 

,

 

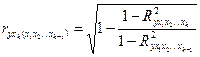где 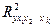- множественный коэффициент детерминации всего комплекса

факторов с результатом;

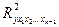- тот же показатель детерминации, но без введения в модель фактора х_k.

 

Пример. Рассмотрим методику корреляционно-регрессионного анализа на примере статистической обработки данных по предприятиям электросвязи

Таблица 2.2