Формулы коэффициентов эластичности

Классы моделей

Типы данных

В эконометрических исследованиях

Парная регрессия и корреляция

Лекция 1.

Эконометрика – это наука, изучающая количественные закономерности и взаимозависимости в экономике методами математической статистики.

Цель эконометрики – эмпирический вывод экономических законов.

Задачи – построение экономических моделей и оценивание их параметров, проверка гипотез о свойствах экономических показателей и формах их связи.

Эконометрический анализ служит основой для экономического анализа и прогнозирования, создавая возможность для принятия обоснованных экономических решений.

 

При моделировании экономических процессов оперируют типами данных: пространственными и временными.

Пространственные данные – это данные по какому-либо экономическому показателю, полученные от разных однотипных объектов (фирм, регионов и т.п.), но относящиеся к одному и тому же моменту времени (пространственный срез). Например, данные об объеме производства, количестве работников, доходе разных фирм в один и тот же момент времени.

Временные данные – это данные, характеризующие один и тот же объект в различные моменты времени (временной срез). Например, ежеквартальные данные об инфляции, средней заработной плате, данные о национальном доходе за последние годы.

 

Главным инструментом эконометрики служит эконометрическая модель. Эконометрические модели могут представлять собой модель временного ряда, систему одновременных уравнений, а также регрессионную модель с одним уравнением. Регрессионная модель с одним уравнением представляет собой уравнение регрессии, где среднее значение зависимой (объясняемой, эндогенной) переменной у объясняется как функция одной или нескольких независимых (объясняющих, экзогенных) переменных:

 

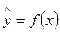или ,

 

где х₁, х₂, ….х_n – независимые переменные или факторы, оказывающие влияние

на зависимую переменную.

Рассмотрим уравнение регрессии: ,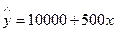

где 10000 – постоянные затраты, не зависящие от объема производства;

500 – переменные затраты, зависящие от объема производства. Подставляя в уравнение регрессии различные значения х (объем производства) можно получить общее значение затрат на производство. Таким образом, мы имеем дело с эконометрической моделью, которая позволяет делать прогнозы, однако для этого необходимо предварительно построить эту модель и оценить ее.

Наиболее простым является построение и оценка парной регрессии.

Парная регрессия – это уравнение связи двух переменных y и x:

 

.

 

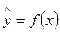Различают линейные и нелинейные регрессии.

Линейная регрессия имеет вид: ,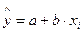

где a – параметр, представляющий собой значение y при x=0. Если фактор не имеет или не может иметь нулевого значения, то вышеуказанная трактовка не имеет смысла. Параметр 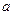может и не иметь экономического содержания.

b – коэффициент регрессии, который указывает направление связи (если 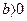, связь прямая, если , связь обратная). Величина b показывает, на какую величину в среднем изменится результат, если фактор х увеличится на одну единицу своего измерения.

Практически в каждом отдельном случае величина у складывается из двух слагаемых:

 

,

 

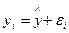где у_i – фактическое значение результативного признака;

_x - теоретическое значение результативного признака, найденное по уравнению регрессии.

- случайная составляющая, характеризующая отклонения реального значения результативного признака от теоретического, найденного по уравнению регрессии.

Построение уравнения регрессии сводится к оценке ее параметров. Для оценки параметров регрессий, линейных по параметрам используют метод наименьших квадратов, который позволяет получить такие оценки параметров, что при которых сумма квадратов отклонений фактических значений результативного признака у от теоретических минимальна, т.е. .

Для этого решается следующая система нормальных уравнений относительно a и b:

 

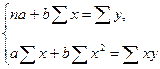
Можно воспользоваться готовыми формулами, которые вытекают из данной системы:

 

,

,

 

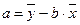где 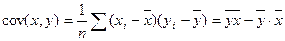− ковариация двух переменных x, y , т.е. средняя величина произведения отклонений этих переменных от своих средних;

− дисперсия фактора (объясняющей переменной) x.

Пример. По группе предприятий, выпускающих один и тот же вид продукции, рассматривается функция издержек 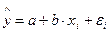. Необходимая для расчета оценок параметров информация представлена в таблице 1.1.

Таблица 1.1

Расчетная таблица

Номер предприятия	Выпуск продукции, тыс. ед. х	Затраты на производство, млн. руб. у
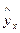
						31,1 67,9 141,6 104,7 178,4 104,7 141,6
Итого

 

Система нормальных уравнений будет иметь вид:

 

 

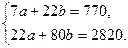
Решив ее, получим:

.

Уравнение регрессии примет вид:

Коэффициент регрессии при этом отражает, что с увеличением выпуска продукции на 1 тыс. ед. издержки возрастают в среднем на 36,84 млн. руб., то есть дополнительный прирост продукции на одну единицу своего измерения потребует увеличения затрат на производство продукции в среднем на 36,84 млн. руб.

Подставив в уравнение значения х, найдем теоретические значения у. В данном случае параметр не имеет экономического смысла. В рассматриваемом примере также имеем следующие значения средних квадратических отклонений в ряду х и у:

 

;

;

.

 

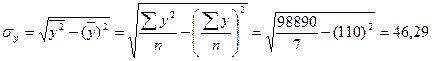Ниже представлен расчет относительного показателя вариации: коэффициент вариации:

 

;

.

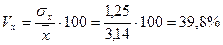То, что ‹ 0, соответствует опережению изменения результата над изменением фактора: .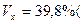

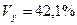Тесноту связи изучаемых явлений оценивает линейный коэффициент парной корреляции 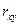для линейной регрессии 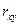(-1 ≤ ≤ 1):

 

,

 

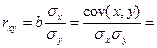
где 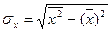- среднее квадратическое отклонение в ряду x,

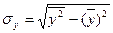- среднее квадратическое отклонение в ряду y.

Линейный коэффициент корреляции как измеритель тесноты линейной связи признаков связан не только с коэффициентом регрессии b, но и с коэффициентом эластичности, который является показателем силы связи, выраженным в процентах.

Коэффициент эластичности отражает, на сколько процентов изменится значение y при изменение значения фактора на 1%. Коэффициент эластичности рассчитывается как .

Обобщающий (средний) коэффициент эластичности рассчитывается для среднего значения :

 

 

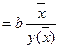
и показывает, на сколько процентов изменится y относительно своего среднего уровня при росте x на 1% относительно своего среднего уровня.

Точечный коэффициент эластичности рассчитывается для конкретного значения x=x₀:

 

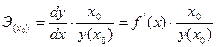
и показывает, на сколько процентов изменится y относительно своего уровня y(x₀) при увеличении 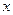на 1% от уровня x₀.

На основе данных примера рассчитаем коэффициент корреляции и средний коэффициент эластичности.

.

Полученный показатель близок к единице, следовательно между х и у связь весьма сильная, кроме того, так как полученное значение больше 0, то связь между х и у прямая.

Средний коэффициент эластичности при значении х равном 3,14 составит:

. Показатель при расчете сразу получается в процентах, умножать на 100% не нужно.

Средний коэффициент эластичности отражает, что с ростом средней величины факторного признака х на 1% среднее значение результативного признака возрастает в среднем на 1,053%.

Для оценки качества подбора линейной функции рассчитывается коэффициент детерминации. Коэффициент детерминации – это квадрат линейного коэффициента парной корреляции; он характеризует долю дисперсии результативного признака у, объясняемую регрессией, в общей дисперсии результативного признака:

,

 

где 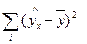- сумма квадратов отклонений, обусловленная регрессией

(факторная);

- общая сумма квадратов отклонений.

 

Чем больше доля объясненной вариации, тем соответственно меньше роль прочих факторов и, следовательно, линейная модель хорошо аппроксимирует исходные данные, и ею можно воспользоваться для прогноза значений результативного признака. Иначе, чем ближе коэффициент детерминации к 1, тем в большей степени уравнение регрессии пригодно для прогнозирования.

После того как уравнение линейной регрессии найдено, проводится оценка значимости как уравнения в целом, так и отдельных его параметров.

Проверка значимости уравнения регрессии осуществляется путем расчета F-критерия Фишера. F-тест состоит в проверке гипотезы Н₀ о статистической незначимости уравнения регрессии и показателя тесноты связи. Непосредственному расчету F-критерия предшествует анализ дисперсии. Центральное место в нем занимает разложение общей суммы квадратов отклонений на две части: объясненную (факторную) и остаточную:

 

,

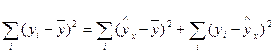где - остаточная сумма квадратов отклонений.

 

Любая сумма квадратов отклонений связана с числом степеней свободы df, т.е. с числом свободы независимого варьирования признака. Число степеней свободы связано с числом единиц совокупности n и с числом определяемых по ней констант. Применительно к исследуемой проблеме число степеней свободы должны показать, сколько независимых отклонений из n возможных 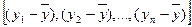требуется для образования данной суммы квадратов. Так, для общей суммы квадратов 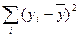необходимо (n-1) независимых отклонений, ибо по совокупности из n единиц после расчета среднего уровня свободно варьируют лишь (n-1) число отклонений. Например, имеем ряд значений у: 1, 2, 3, 4, 5.

, и тогда n отклонений от среднего составят: -2; -1; 0; 1; 2. Поскольку сумма отклонений равна нулю (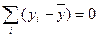), то свободно варьируют лишь четыре отклонения, а пятое отклонение может быть определено, если четыре предыдущие известны.

При расчете объясненной, или факторной, суммы квадратов 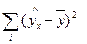используются теоретические (расчетные) значения результативного признака, найденные по линии регрессии. При заданном объеме наблюдений по х и у факторная сумма квадратов при линейной регрессии зависит только от одной константы коэффициента регрессии b, то данная сумма квадратов имеет одну степень свободы.

Существует равенство между числом степеней свободы общей, факторной и остаточной суммами квадратов. Число степеней свободы остаточной суммы квадратов при линейной регрессии составляет n-2. Число степеней свободы для общей суммы квадратов определяется числом единиц, и поскольку мы используем среднюю вычисленную по данным выборки, то теряем одну степень свободы, т.е. df_общ = n – 1.

Разделив каждую сумму квадратов на соответствующее ей число степеней свободы, получим средний квадрат отклонений или дисперсию на одну степень свободы:

 

; ; .

 

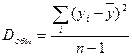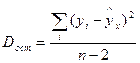Определение дисперсии на одну степень свободы приводит дисперсии к сравниваемому виду. Сопоставляя факторную и остаточную дисперсии на одну степень свободы, получим величину F-отношения, т.е. критерий F:

.

 

При линейной связи возможно использование формул:

 

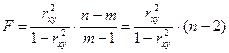или ,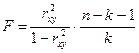

 

где m – число параметров в уравнении регрессии;

(m-1) – число степеней свободы для факторной дисперсии;

n – число наблюдений;

(n-m) – число степеней свободы для остаточной дисперсии;

k – количество коэффициентов регрессии в уравнении регрессии.

Вместо числа параметров уравнения регрессии m можно использовать число коэффициентов регрессии k, которое на единицу меньше m, т.е. k=(m−1).

Вычисленное значение F-отношения признается достоверным (отличным от единицы), если оно больше табличного значения F-критерия. В этом случае нулевая гипотеза об отсутствии связи признаков отклоняется и делается вывод о существенности этой связи:

 

F_табл‹ F_факт, гипотеза Н₀ отклоняется.

 

F_табл – это максимально возможное значение критерия под влиянием случайных факторов при данных степенях свободы () и уровне значимости , который принимается равным 0,05 или 0,01.

Если же величина F окажется меньше табличной, то вероятность нулевой гипотезы выше заданного уровня и она не может быть отклонена без риска сделать неправильный вывод о наличии связи.

Продолжая рассмотрение примера, рассчитаем коэффициент детерминации и F-критерий Фишера.

− высокое значение коэффициент детерминации говорит о пригодности уравнения регрессии для прогнозирования.

В таблицу дисперсионного анализа подставим значения сумм квадратов отклонений.

Таблица 1.2

Расчетная таблица для определения общей суммы квадратов отклонений

Затраты на производство, млн. руб. у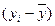
	-80
	-40
	-10
	-10
	×

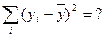
Таблица 1.3

Расчетная таблица для определения факторной суммы квадратов отклонений

Теоретические значений результативного признака
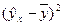
31,1	-78,9	6225,21
67,9	-42,1	1772,41
141,6	31,6	998,56
104,7	-5,3	28,09
178,4	68,4	4678,56
104,7	-5,3	28,09
141,6	31,6	998,56
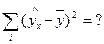
	×	14729,48

Таблица 1.4

Расчетная таблица для определения остаточной суммы квадратов отклонений

Затраты на производство, млн. руб. у	Теоретические значений результативного признака
	31,1	-1,1	1,21
	67,9	2,1	4,41
	141,6	8,4	70,56
	104,7	-4,7	22,09
	178,4	-8,4	70,56
	104,7	-4,7	22,09
	141,6	8,4	70,56
	×	×	261,48

Таблица 1.5

Расчетная таблица

Источ- ник вариа-ци	Сумма квадратов отклонений	Число степе-ней свобо-ды	Дисперсия на одну степень свободы (средний квадрат отклонений)	F-критерий
Общая		n – 1= =7−1=6		-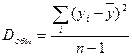
Фактор-ная		m – 1= =2−1= =1
Остаточ-ная		n – m= =7−2= =5		-

 

F_табл=6,61 при уровне значимости равным 0,05 и .

F_табл ‹ F_факт

Следовательно можно сделать вывод о значимости уравнения регрессии.

Расчет F-критерия Фишера можно также провести следующим образом:

.

В данном случае более высокое значение показателя обусловлено тем, что при расчете значения очень сильно округляются и точность такого способа расчета бает меньше чем расчет через дисперсионный анализ.

Для упрощения расчетов сумм квадратов отклонений также можно использовать следующие формулы:

 

,

.

 

где − дисперсия результативного признака.

Для оценки статистической значимости коэффициентов регрессии и корреляции рассчитываются t-критерий Стьюдента и доверительные интервалы каждого из показателей. Выдвигается гипотеза Н₀ о случайной природе показателей, т.е. о незначимом их отличии от нуля. Оценка значимости коэффициентов регрессии и корреляции с помощью t-критерия Стьюдента проводится путем сопоставления их значений с величиной стандартной ошибки:

 

; .

 

Стандартные ошибки параметров линейной регрессии и коэффициент корреляции определяются по формулам:

 

,

 

где S² – остаточная дисперсия на одну степень свободы;

 

;

 

Сравнивая фактическое t_факт и критическое (табличное) значения t-статистики t_табл (при определенном уровне значимости и числе степеней свободы (n-2)) – принимаем или отвергаем гипотезу Н₀. Если t_табл < t_факт, то Н₀ отклоняется, т.е. a, b, r_xy не случайно отличаются от нуля и сформировались под влиянием систематически действующего фактора х. Если t_табл > t_факт, то гипотеза Н₀ не отклоняется и признается случайная природа формирования a, b, r_xy.

Рассмотренную формулу оценки коэффициента корреляции рекомендуется применять при большом числе наблюдений, а также если r_xy не близко к +1 или –1. Если же величина r_xy близка к +1, то распределение его оценок отличается от нормального, или распределения Стьюдента, так как величина коэффициента корреляции ограничена значения от –1 до +1. Для устранения данного затруднения Р.Фишер ввел вспомогательную величину z, связанную с r_xy следующим соотношением: . При изменении r_xy от –1 до +1 величина z изменятся от до , что соответствует нормальному распределению.

Стандартная ошибка величины z рассчитывается по формуле:

 

.

 

Для расчета доверительного интервала определяем предельную ошибку для каждого показателя:

 

 

Формулы для расчета доверительных интервалов имеют следующий вид:

 

; ; ;

; ; .

 

Если в границы доверительного интервала попадает ноль, т.е. нижняя граница отрицательна, а верхняя положительна, то оцениваемый параметр принимается нулевым, так как он не может одновременно принимать и положительное, и отрицательное значения.

Прогнозное значение y_p определяется путем подстановки в уравнение регрессии соответствующего (прогнозного) значения x_p. Вычисляется стандартная ошибка прогноза :

 

.

 

Величина стандартной ошибки достигает минимума при x_p=и возрастает по мере того, как «удаляется» от в любом направлении. Можно ожидать наилучшие результаты прогноза, если признак-фактор находится в центре области наблюдений х.

Доверительный интервал прогноза:

 

; ; ,

 

где .

 

Однако так как фактические значений у варьируют около среднего значения , индивидуальные значения у могут отклоняться от на величину случайно ошибки , дисперсия которой оценивается как остаточная дисперсия на одну степень свободы S². Поэтому ошибка предсказываемого индивидуального значения у должна включать не только стандартную ошибку, но и случайную ошибку. Средняя ошибка прогнозируемого индивидуального значения составит:

 

.

 

На основе данных примера рассмотрим значения t-критерий Стьюдента.

;

Таблица 1.6

Расчетная таблица

х
	-2,14	4,5796
	-1,14	1,2996
	0,86	0,7396
	-0,14	0,0196
	1,86	3,4596
	-0,14	0,0196
	0,86	0,7396
	×	10,8572

 

Также расчет можно осуществить через F-критерий Фишера:

.

t_табл =2,57 при уровне значимости =0,05 и числе степеней свободы 5.

t_табл < t_b следовательно Н₀ отклоняется, т.е. b и r_xy не случайно отличаются от нуля и сформировались под влиянием систематически действующего фактора х.

Доверительные интервалы примут значения:

;

.

31,21 ≤ b ≤ 42,47.

Значение коэффициента регрессии не проходит через нуль.

Коэффициент корреляции также сформировался под влиянием систематически действующего фактора.

.

t_табл =2,57 при уровне значимости =0,05 и числе степеней свободы 5.

t_табл < t_а следовательно гипотеза Н₀ не отклоняется.

Доверительные интервалы примут значения:

;

.

−25 ≤ а ≤ 13,27.

Таким образом, параметр а проходит через ноль, следовательно подтверждается несущественность параметра.

Рассчитаем доверительный интервал прогноза, чтобы иметь представление о том, какое значение примет теоретическое значение результативного признака при определенном значении х.

Пусть х_пр=4, тогда

.

 

Доверительный интервал прогноза:

 

;

.

 

Диапазон между верхней и нижней границей доверительного интервала составляет 1,13 (150,15:132,99).

 

Если между экономическими явлениями существуют нелинейные соотношения, то они выражаются с помощью соответствующих нелинейных функций.

Нелинейные регрессии делятся на два класса:

v регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам;

v регрессии, нелинейные по оцениваемым параметрам.

Регрессии, нелинейные по объясняющим переменным:

· полиномы разных степеней:

;

· равносторонняя гипербола:

.

Применение МНК для оценки параметров параболы второй степени приводит к следующей системе нормальных уравнений:

при построении уравнения регрессии вида гиперболы строится и решается следующая система нормальных уравнений:

Для удобства решения прибегают к процедуре линеаризации.

Линеаризация, которая состоит в замене нелинейных объясняющих переменных новыми линейными переменными, приводит нелинейную регрессию к виду линейной. Например, в параболе второй степени: , заменяем переменную х² на z, и получаем двухфакторное уравнение линейной регрессии: .

Полином любого порядка может быть сведен к линейной регрессии с последующим применением методов оценивания параметров и проверки гипотез.

Среди класса нелинейных функций, параметры которых без особых затруднений оцениваются с помощью метода наименьших квадратов (МНК), выступает равносторонняя гипербола: , которая может быть использована, например, для характеристики связи удельных расходов сырья, материалов и топлива с объемом выпускаемой продукции.

Линеаризация происходит путем замены на z, что приводит к линейному уравнению регрессии вида: .

Формула критерия Фишера для параболы имеет вид:

 

,

 

для гиперболы:

 

.

Регрессии нелинейные по оцениваемым параметрам представлены ниже:

· степенная – ;

· показательная – ;

· экспоненциальная – .

Класс нелинейных моделей подразделяется на внутренне линейные и внутренне нелинейные. Если линейная модель внутренне линейна, то с помощью соответствующих преобразований она может быть приведена к линейному виду.

Степенная функция является примером нелинейной по параметрам регрессии. Данная модель нелинейна относительно оцениваемых параметров, т.к. включает параметры a и b неаддитивно. Однако ее можно считать внутренне линейной, так как логарифмирование приводит его к линейному виду: .

При исследовании взаимосвязей среди функций, использующих ln y, в эконометрике преобладают степенные зависимости – это кривые спроса и предложения, кривые освоения для характеристики связи между трудоемкостью продукции и масштабами производства в период освоения выпуска нового вида изделий, а также зависимость валового национального дохода от уровня занятости.

Для оценки параметров степенной функции применяется МНК к линеаризованному уравнению , т.е. решается система нормальных уравнений:

Параметр b определяется непосредственно из системы, а параметр a – косвенным путем после потенцирования величины ln a.

Так как в виде степенной функции изучается не только эластичность спроса, но и предложения, то обычно параметром b<0 характеризуется эластичность спроса, а параметром b>0 – эластичность предложения.

Если же модель представить в виде:

 

,

 

То она становится внутренне нелинейной, так как ее невозможно превратить в линейный вид, то же относится к моделям вида:

 

,

 

так как эти уравнения не могут быть преобразованы в уравнения , линейные по коэффициентам.

Ниже представлены формулы расчета коэффициентов эластичности (табл. 1.7).

 

Таблица 1.7.

Вид функции	Точечный коэффициент эластичности	Средний коэффициент эластичности
Линейная
Парабола
Равносторонняя гипербола
Степенная
Показательная

 

Уравнение нелинейной регрессии дополняется показателем корреляции, а именно индексом корреляции (0 ≤ ≤ 1):

 

.

 

Проверка статистической значимости уравнения нелинейной регрессии в целом осуществляется через F-критерий Фишера и индекс детерминации R².

Индекс детерминации используется для проверки статистической значимости в целом уравнения нелинейной регрессии.

Так для степенной функции вида значение m = 1 и формула F-критерия принимает вид, что и при линейной зависимости:

 

.

 

Средняя ошибка аппроксимации – это среднее отклонение расчетных значений результативного признака от фактических:

.

 

Ошибка аппроксимации в пределах 5-7% свидетельствует о хорошем подборе модели к исходным данным.