МЕТРИЧЕСКИЕ ЗАДАЧИ
ЛЕКЦИЯ 9
Определение значений измеряемых величин
(длины отрезка, угла …)
Задача 1: Определить расстояние от точки С до прямой АВ





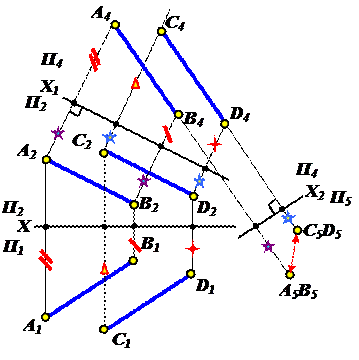
Задача 2:Определить расстояние между параллельными прямыми
Чтобы определить расстояние между параллельными прямыми, необходимо прямые общего положения преобразовать в проецирующие прямые
Задача 3: Определить расстояние между скрещивающимися прямыми




















































Чтобы определить расстояние между скрещивающимися прямыми, необходимо одну из прямых (CD) преобразовать в проецирующую прямую.
Задача 4: Определить натуральную величину двугранного угла между плоскостями β(ΔАВС) и γ(ΔАСD)
Для определения двугранного угла необходимо общую сторону двух плоскостей (АD) преобразовать в проецирующую прямую.
Задача 5: Определить расстояние от точки D до плоскости α(ΔАВС)
а) метод плоскопараллельного перемещения:
б) метод замены плоскостей:

Чтобы определить расстояние от точки до плоскости, необходимо:
1. Плоскость общего положения (ΔАВС) преобразовать в проецирующую плоскость (ΔА′2В′2С′2).
2. Опустить перпендикуляр из точки D′2 к плоскости α(ΔА′2В′2С′2).
3. Длина перпендикуляра – это расстояние от точки D до плоскости α(ΔАВС)
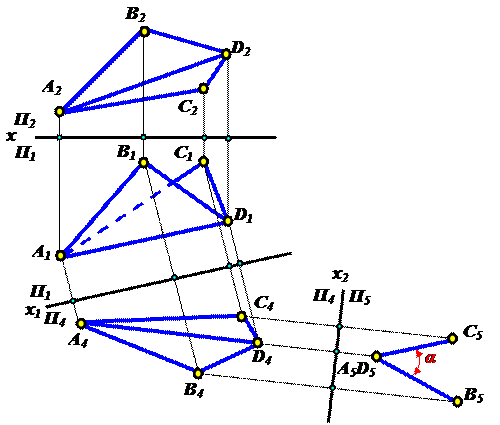
Задача 6:
Заданы две проекции пирамиды. Определить:
• Натуральную величину грани ABC и угол ее наклона к П1 (α);
• Расстояние от вершины S до грани АВС (y);
• Расстояние от ребра ВС до ребра AS (x);
• Расстояние от точки А до ребра BS (z).
Рекомендации к выполнению:
- Для построения натуральной величины грани ABC необходимо применить
третью и четвертую задачи преобразования чертежа (лекция 7);
- Нахождение расстояния от вершины до грани показано в задаче 5б
(лекция 9);
- Нахождение расстояния от ребра до ребра показано в задаче 3 (лекция 9);
- Нахождение расстояния от точки до ребра показано в задаче 1 (лекция 9).