Линейная регрессия и корреляция
Рисунок 2.1 - Основные типы кривых, используемые при количественной оценке связей между двумя переменными
Аналитический метод выбора типа уравнения регрессии основан на изучении материальной природы связи исследуемых признаков.
Экспериментальный метод основан на сравнении показателей качества, рассчитанных при разных моделях (например, путем сравнения величины остаточной дисперсии).
Если уравнение регрессии проходит через все точки корреляционного поля, что возможно только при функциональной связи, когда все точки лежат на линии регрессии  , то фактические значения результативного признака совпадают с теоретическими
, то фактические значения результативного признака совпадают с теоретическими  , т.е. они полностью обусловлены влиянием фактора
, т.е. они полностью обусловлены влиянием фактора 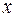 . В этом случае остаточная дисперсия
. В этом случае остаточная дисперсия  . В практических исследованиях, как правило, имеет место некоторое рассеяние точек относительно линии регрессии. Оно обусловлено влиянием прочих, не учитываемых в уравнении регрессии, факторов. Иными словами, имеют место отклонения фактических данных от теоретических
. В практических исследованиях, как правило, имеет место некоторое рассеяние точек относительно линии регрессии. Оно обусловлено влиянием прочих, не учитываемых в уравнении регрессии, факторов. Иными словами, имеют место отклонения фактических данных от теоретических  . Величина этих отклонений лежит в основе расчета остаточной дисперсии:
. Величина этих отклонений лежит в основе расчета остаточной дисперсии:
 . (2.2)
. (2.2)
Чем меньше величина остаточной дисперсии, тем меньше влияние не учитываемых в уравнении регрессии факторов и тем лучше уравнение регрессии подходит к исходным данным.
Считается, что число наблюдений должно в 7-8 раз превышать число рассчитываемых параметров при переменной 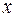 . Это означает, что искать линейную регрессию, имея менее 7 наблюдений, вообще не имеет смысла. Если вид функции усложняется, то требуется увеличение объема наблюдений.
. Это означает, что искать линейную регрессию, имея менее 7 наблюдений, вообще не имеет смысла. Если вид функции усложняется, то требуется увеличение объема наблюдений.
Линейная регрессия находит широкое применение в эконометрике ввиду четкой экономической интерпретации ее параметров.
Линейная регрессия сводится к нахождению уравнения вида
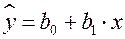 . (2.3)
. (2.3)
Уравнение вида (2.3) позволяет по заданным значениям фактора 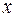 находить теоретические значения результативного признака, подставляя в него фактические значения фактора
находить теоретические значения результативного признака, подставляя в него фактические значения фактора 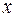 (рис. 2.2).
(рис. 2.2).

Рисунок 2.2 – Графическая интерпретация параметров линейной регрессии
Параметр 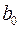 определяется как точка пересечения линии регрессии с осью Оy, а параметр
определяется как точка пересечения линии регрессии с осью Оy, а параметр  исходя из угла наклона линии регрессии как
исходя из угла наклона линии регрессии как  , где
, где  - приращение результата y,
- приращение результата y, 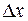 - приращение фактора х.
- приращение фактора х.
Построение линейной регрессии сводится к оценке ее параметров – 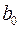 и
и  . Классический подход к оцениванию параметров линейной регрессии основан на методе наименьших квадратов (МНК). МНК позволяет получить такие оценки параметров
. Классический подход к оцениванию параметров линейной регрессии основан на методе наименьших квадратов (МНК). МНК позволяет получить такие оценки параметров 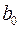 и
и  , при которых сумма квадратов отклонений фактических значений результативного признака
, при которых сумма квадратов отклонений фактических значений результативного признака 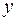 от теоретических
от теоретических 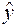 минимальна:
минимальна:
 . (2.4)
. (2.4)
 Т.е. из всего множества линий линия регрессии на графике выбирается так, чтобы сумма квадратов расстояний по вертикали между точками и этой линией была бы минимальной (рис. 2.3).
Т.е. из всего множества линий линия регрессии на графике выбирается так, чтобы сумма квадратов расстояний по вертикали между точками и этой линией была бы минимальной (рис. 2.3).
Рисунок 2.3 - Линия регрессии с минимальной дисперсией остатков
Как известно из курса математического анализа, чтобы найти минимум функции (2.4), надо вычислить частные производные по каждому из параметров 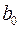 и
и  и приравнять их к нулю. Обозначим
и приравнять их к нулю. Обозначим 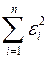 через
через  , тогда:
, тогда:  .
.
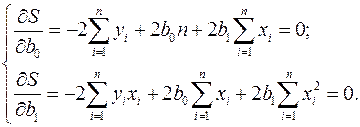
После преобразований, получим следующую систему линейных уравнений для оценки параметров 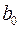 и
и  :
:
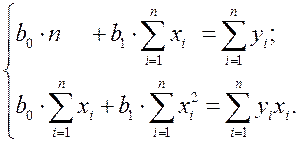 (2.5)
(2.5)
Решая систему уравнений (2.5), найдем искомые оценки параметров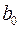 и
и  . Можно воспользоваться следующими формулами, которые следуют непосредственно из решения системы (2.5):
. Можно воспользоваться следующими формулами, которые следуют непосредственно из решения системы (2.5):
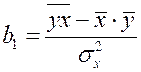 , (2.6)
, (2.6)
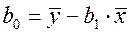 , (2.7)
, (2.7)
где 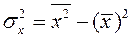 – дисперсия признака
– дисперсия признака 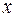 ; (2.8)
; (2.8)
 ,
,  ,
,  ,
, 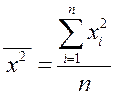 .
.
Дисперсия – характеристика случайной величины, определяемая как математическое ожидание квадрата отклонения случайной величины от ее математического ожидания. Математическое ожидание – сумма произведений значений случайной величины на соответствующие вероятности.
Параметр  называется коэффициентом регрессии. Его величина показывает среднее изменение результата с изменением фактора на одну единицу. Знак при коэффициенте регрессии показывает направление связи: при b1 > 0, связь прямая, а при b1 < 0 – связь обратная.
называется коэффициентом регрессии. Его величина показывает среднее изменение результата с изменением фактора на одну единицу. Знак при коэффициенте регрессии показывает направление связи: при b1 > 0, связь прямая, а при b1 < 0 – связь обратная.
Формально b0 – значение 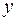 при
при  . Если признак-фактор
. Если признак-фактор 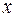 не может иметь нулевого значения, то вышеуказанная трактовка свободного члена b0 не имеет смысла, т.е. параметр b0 может не иметь экономического содержания. Попытки экономически интерпретировать параметр b0 могут привести к абсурду, особенно при b0 < 0. Если b0 > 0, то относительное изменение результата происходит медленнее, чем изменение фактора, т.е.
не может иметь нулевого значения, то вышеуказанная трактовка свободного члена b0 не имеет смысла, т.е. параметр b0 может не иметь экономического содержания. Попытки экономически интерпретировать параметр b0 могут привести к абсурду, особенно при b0 < 0. Если b0 > 0, то относительное изменение результата происходит медленнее, чем изменение фактора, т.е. 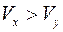 , где
, где  - коэффициент вариации признака х;
- коэффициент вариации признака х; 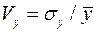 - коэффициент вариации признака y.
- коэффициент вариации признака y.
Для оценки тесноты линейной связи между двумя признаками рассчитывают линейный коэффициент парной корреляции  :
:
 , (2.9)
, (2.9)
где  - среднее квадратическое отклонение признака х;
- среднее квадратическое отклонение признака х;
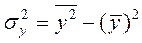 - дисперсия признака y; (2.10)
- дисперсия признака y; (2.10)
 - среднее квадратическое отклонение признака y.
- среднее квадратическое отклонение признака y.
Среднее квадратическое отклонение – в теории вероятностей и статистике наиболее распространенный показатель рассеивания значений случайной величины относительно ее математического ожидания. Измеряется в единицах измерения самой случайной величины. Равно корню квадратному из дисперсии случайной величины. Среднее квадратическое отклонение показывает, на сколько в среднем величина изучаемого признака у отдельных единиц совокупности отличается от среднего значения признака в совокупности.
Линейный коэффициент парной корреляции находится в пределах: 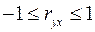 . Чем ближе абсолютное значение
. Чем ближе абсолютное значение  к единице, тем сильнее линейная связь между признаками (при
к единице, тем сильнее линейная связь между признаками (при  имеем строгую функциональную зависимость). Если ryx = 0, линейная связь между y и x отсутствует. Если
имеем строгую функциональную зависимость). Если ryx = 0, линейная связь между y и x отсутствует. Если  , линейная связь между y и x слабая; если
, линейная связь между y и x слабая; если  , линейная связь между y и x средняя; если
, линейная связь между y и x средняя; если  , линейная связь между y и x тесная.
, линейная связь между y и x тесная.
Близость абсолютной величины линейного коэффициента корреляции к нулю еще не означает отсутствия связи между признаками. При другой (нелинейной) спецификации модели связь между признаками может оказаться достаточно тесной.
Для оценки качества подбора функции рассчитывается коэффициент детерминации, характеризующий долю дисперсии результативного признака 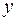 , объясняемую регрессией, в общей дисперсии результативного признака:
, объясняемую регрессией, в общей дисперсии результативного признака:
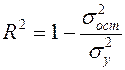 . (2.11)
. (2.11)
Величина  характеризует долю дисперсии
характеризует долю дисперсии 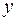 , вызванную влиянием остальных не учтенных в модели факторов.
, вызванную влиянием остальных не учтенных в модели факторов.
Линейный коэффициент детерминации может быть рассчитан как квадрат линейного коэффициента корреляции:  .
.