Введение в эконометрическое моделирование

Влияние на качество модели множественной регрессии избы-

СОДЕРЖАНИЕ

 

1. Введение в эконометрическое моделирование……………………………….

1.1. Эконометрическая модель и экспериментальные данные…………………

1.2. Этапы эконометрического моделирования………………………………….

2. Регрессионная модель. Общие положения……………………………………

3. Парная линейная регрессия…………………………………………………….

3.1. Вид уравнения и предпосылки для регрессионного анализа………………

3.2.Отыскание оценок параметров парной регрессии…………………………..

3.3. Оценка значимости уравнения и его параметров……………………………

4. Множественная линейная регрессия…………………………………………...

4.1. Матричная форма регрессионной модели…………………………………..

4.2. Отбор факторов для моделей множественной регрессии…………………..

точных переменных и отсутствия существенных переменных…………………

4.4. Оценка параметров модели множественной регрессии…………………….

4.5. Оценка надёжности результатов множественной регрессии……………....

5. Нелинейная парная регрессия………………………………………………….

5.1. Функции и их характеристики……………………………………………….

5.2 Корреляция при нелинейной регрессии………………………………………

6. Модели ANCOVA (модели ковариационного анализа). Фиктивные переменные……………………………………………………………………………...

7. Оценка точности регрессионных моделей……………………………………

8. Гетероскедастичность остатков………………………………………………..

8.1. Сущность и причины гетероскедастичности………………………………..

8.2. Выявление гетероскедастичности……………………………………………

8.3. Устранение гетероскедастичности…………………………………………..

9. Автокорреляция в остатках…………………………………………………….

9.1 Сущность и причины автокорреляции в остатках…………………………..

9.2. Обнаружение автокорреляции в остатках……………………………………

9.3. Методы устранения автокорреляции…………………………………………

10. Системы одновременных уравнений………………………………………….

10.1. Виды переменных и уравнений СОУ……………………………………….

10.2. Проблемы идентификации…………………………………………………..

10.3. Оценивание параметров структурной модели……………………………..

11. Динамические эконометрические модели……………………………………

11.1. Интерпретация параметров модели с распределенным лагом…………….

11.2. Интерпретация параметров модели авторегрессии………………………..

11.3. Соображения о выборе лаговых структур в модели с распределенным лагом………………………………………………………………………………...

11.4. Полиномиальные лаговые структуры Алмон………………………………

11.5. Геометрические структуры Койка………………………………………….

11.6. Оценка параметров авторегрессионных моделей первого порядка (AR(1)–моделей)……………………………………………………………………

11.7. Модель адаптивных ожиданий……………………………………………...

12. Сглаживание временных рядов………………………………………………..

12.1. Метод скользящей средней………………………………………………….

12.2. Регрессионная модель и метод конечных разностей………………………

12.3. Стационарные и нестационарные временные ряды……………………….

12.4. Преобразования ARMA и ARIMA………………………………………….

13. Моделирование временного ряда при наличии структурных изменений…………………………………………………………………………………..

14. Статистико-математические таблицы……………………………………

 

 

Эконометрика - это наука, которая даёт количественное выражение взаимосвязей экономических или иных явлений и процессов, раскрытых экономической или иной теорией.

Пусть требуется определить величину, формирующуюся под воздействием нескольких независимых факторов. Такую величину называют объясняемой пе­ременной (функцией) или результативным признаком, а факторы – объясняющими перемен­ными (аргументами).

Общей чертой для всех эконометрических моделей является разбиение зави­симой переменной на две составляющие: объясненную и случайную.

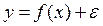или – это модели с аддитивным и мультипликативным остатком, соответственно. Пусть имеется p объясняющих переменных X₁, X₂,…, X_p и зависимая переменная Y. Переменная Y – случайная величина, имеющая при заданных значениях факторов из вектора x некоторое статистическое распределение f x₁, x₂,…, x_p (y); чаще всего это распределение нормально, но иногда это предположение бывает неправомерно.

Объясняющие переменные можно считать как случайными, так и детер­минированными. Классические модели предполагают, что они детерминированы. Опыт показывает, что результаты такого подхода мало отличаются от случаев, если X_j считать случайными. Наиболее естественным выбором объясняемой части ре­зультативного признака Y является его условное математическое ожидание.

Mx₁, x₂, x₃,…, x_p(Y).

Статистические данные для построения модели представляются табл. 1.1 наблюдений, которая приводится ниже для p переменных и n наблюдений. В этой же таблице после соответствующих вычислений приводят теоретические (модельные) значения объясняемой переменной в каждом наблюдении и остатки ε – также для каждого наблюдения.

таблица 1.1

			…
			…
…	…	…	…	…	…	…	…
			…

 

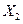
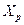
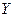
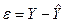
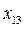
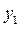
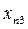
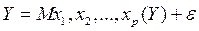− уравнение регрессионной модели с аддитивным остатком (такие модели наиболее употребительны).

Эконометриче­ская модель не всегда является регрессионной, то есть объясненная часть не всегда является условным математическим ожиданием. Это может произойти тогда, когда объясненная составляющая содержит систематическую ошибку.

Рассмотрим равенство и возьмём при каждом заданном значении вектора x математическое ожидание от обеих частей:

то есть математическое ожидание от остатка равно нулю.

Таким образом, видно, что остатки имеют нулевое среднее в каждом на­блюдении и не коррелируют с объясняющими переменными. Последнее обстоя­тельство − это наиболее существенное условие состоятельности результатов анали­за эконометрической модели.

1.1. Эконометрическая модель и экспериментальные данные

 

Для получения достаточно достоверных и информативных данных о распреде­лении вектора случайной величины необходимо иметь достаточно большую выборку.

Выборка представляет собой совокупность наборов (векторов) значений

Как правило, число наблюдений велико и значительно превосходит число фак­торных переменных. Опыт показывает, что для получения хороших результатов должно выполняться условие а для получения удовлетворительных результатов должно выпол­няться условие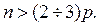

Существует такая проблема: наблюдения y_i, которые при различных наборах объясняющих переменных рассматриваются как реализации случайных величин Y_i, могут в общем случае иметь различные распределения, а это означает, что в конкретной таблице наблюдений для каждой случайной величины будет иметься только одно наблюдение.

В классической эконометрике рассматривают два вида данных:

1. Пространственная выборка или перекрёстные данные (cross-sectional data) – это набор значений показателей, полученный в некоторый момент или за достаточно короткий интервал времени. Таким образом, для пространственной выборки можно говорить, что все ее наблюдения получены примерно в одинаковых условиях.

По другому: пространственная выборка – это серия из n независимых на­блюдений (p+1) – мерной случайной величины.

В дальнейшем X_i можно не рассматривать как случайные величины. Если слу­чайные величины Y_i для различных i независимы, то это влечёт за собой некоррелиро­ванность остатков: Реально проверить, является ли выборка совокупностью независимых наблюдений весьма непросто. Обычно за независимые наблюдения принимают наблюдения, о которых предполагают, что они независимые причинно.

2. Временной или динамический ряд (time-series data) – это выборка наблюде­ний, в которой важны не только сами наблюдения, но и порядок следования их друг за другом. При этом предполагается, что тип распределения наблюдаемой случайной величины остается неизменным во времени, но его параметры могут изменяться.

Модели временных рядов оказываются сложнее моделей пространственной выборки, так как наблюдения во временном ряду в общем случае не являются независимыми и ос­татки могут коррелировать друг с другом.

1.2. Этапы эконометрического моделирования

 

1. Постановочный – здесь формируется цель исследования и составляется набор эконометрических переменных моделей. Каждая переменная должна быть теоретиче­ски обоснована и число факторных переменных должно быть по крайней мере в несколько раз меньше числа наблюдений. Факторные переменные не должны быть связаны между собой функциональной или тесной корреляционной связью. Для оценки влияния качественных признаков могут использоваться фиктивные перемен­ные.

2. Априорный – здесь проводится анализ сущности исследуемого объекта, фор­мирование и формализация априорной информации, то есть известной до начала моделирования.

3. Этап параметризации – здесь выполняется собственно моделирование, то есть выбор общего вида модели и выявление входящих в нее связей. Таким образом, на этом этапе решается проблема спецификации модели – выражение в математической форме обнаруженных связей и соотношений, установление состава экзогенных и эндогенных переменных (в том числе лаговых), формулировка исходных предпосылок и ограничений модели.

4. Информационный – на этом этапе осуществляется сбор необходимой статисти­ческой информации с помощью активного или пассивного эксперимента.

5. Этап идентификации модели – здесь осуществляется статистический анализ модели и оценка её параметров (это самый обширный и насыщенный этап).

6. Этап верификации – это этап проверки истинности, адекватности модели. Заметим, что если имеются статистические данные, характеризующие моделируемый объект в данный момент времени и в предшествующие периоды, то для верификации модели, построенной для целей прогноза, достаточно сравнить наблюдаемые значения и вычисленные модельные значения переменных в предшествующие периоды.