Коэффициент детерминации

Коэффициент детерминации R² характеризует качество регрессионной модели. Другими словами коэффициент детерминации показывает, какая доля общей вариации выходной переменной y обусловлена зависимостью её от входной переменной.

Напомним, что значения различных величин, полученных расчетами, мы условились обозначать « ̃».

В случае парной регрессии значения ỹ_i=ã+b̃x_i выражают ординаты точек (x_i,ỹ_i), лежащих на линии регрессии, в то время как точки с координатами (x_i,y_i), вообще говоря, на этой прямой не лежат. Имеет место равенство

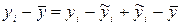Для суммы квадратов отклонений y_i от среднего ` y:

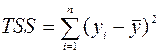
(TSS — total sum of squares) имеем равенство TSS = RSS+ESS, где

— сумма квадратов отклонений, объясненная регрессией (RSS — regression sum of squares),

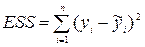
— остаточная сумма квадратов (ESS — error sum of squares).

Коэффициент детерминации определяется по формуле:

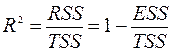(6.1)

Из (6.1) видно, что R²Î[0,1] и чем меньше R² отличается от 1, тем лучше регрессионная модель.

В математической статистике вводится выборочный коэффициент корреляции

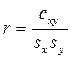
между данными наблюдений (x_i,y_i), i=1, 2, …, n. Напомним (см.4.5), что

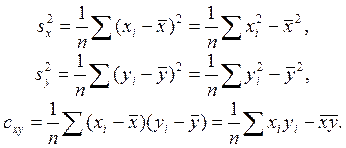
Поскольку (см.4.6)

величину r можно представить в виде

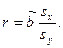
С другой стороны ỹ_i=ã+b̃x_i, `y=ã+b̃`x, откуда следует, что

Поэтому

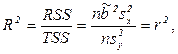
т.е. коэффициент детерминации равен квадрату выборочного коэффициента корреляции.

Заметим, что попутно мы познакомились и с суммами квадратов из последней строчки таблицы из таблицы §5.