Парная линейная регрессия. Метод наименьших квадратов

Корреляция и регрессия

В эконометрических исследованиях часто встречается ситуация, когда каждому значению переменной x соответствует (условное) распределение вероятностей переменной y. Эта зависимость неоднозначна, поэтому в эконометрических исследованиях актуальной является задача поиска закономерностей изменения параметров закона распределения y в зависимости от x. Зависимость между значениями одной из переменных и условным математическим ожиданием другой называется корреляционной зависимостью. В общем случае распределение y может зависеть от x₁, x₂,…, x_n.

Зависимую переменную y называют выходной переменной, независимую называют — входной переменной или регрессором. Уравнения связи между ними называют уравнением регрессии. В случае единственной входной переменной регрессию называют парной, в общем случае — множественной.

По условию вхождения переменных и постоянных коэффициентов (параметров) в уравнение регрессии различают линейную по переменным (или параметрам) и нелинейную.

При исследовании экономических закономерностей законы распределения значений выходной переменной неизвестны. Поэтому для приближенной оценки (аппроксимации) истинной функции регрессии используется выборочный метод.

В современных условиях вычисление коэффициентов корреляционной зависимости можно производить, используя компьютерные программы, например, в MS Excel существуют опции «Регрессия» и «Корреляция», находящиеся в надстройке «Пакет анализа».

Пусть имеется n пар чисел (x_i,y_i), i=1,2,…,n, относительно которых предполагается, что они отвечают линейной зависимости между величинами x и y: y=a+bx , возможно, с некоторой ошибкой e_i, так что

y_i=a+bx_i+e_i, i=1,2,…,n . (4.1)

Какими должны быть наилучшие значения параметров a и b?

Применяя метод наименьших квадратов, мы требуем, чтобы сумма квадратов ошибок e_i была наименьшей:

(4.2)

Подставляя значения e_i из (4.1) в (4.2), получим функцию

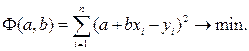
Необходимым условием минимума этой функции, как известно, является равенство нулю ее частных производных по a и b:

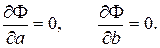
Вычисляя производные, приходим к системе уравнений

(4.3)

Заметим, что эту систему можно записать короче в виде

Система (4.3) равносильна системе

(4.4)

решение которой находится без большого труда:

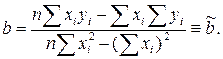
Мы условимся обозначать вычисленные значения параметров как ã и b̃, чтобы отличать их от неизвестных точных значений a и b.

Введем обозначения:

(4.5)

В курсах математической статистики величины `x,`y называются выборочными средними, s²_x — выборочной дисперсией, c_xy — выборочной ковариацией. Теперь формулу для b̃ можно переписать в виде

(4.6)

а выражение для a получается из первого уравнения системы (4.4):

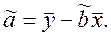
Из этой формулы видно, что точка (`x,`y) лежит на прямой y=ã+b̃x. Поэтому функцию зависимости между величинами x и y можно записать также в виде: y`-y= b̃(x`-x).