МУЛЬТИКОЛЛИНЕАРНОСТЬ.

Предположим, что мы рассматриваем регрессионное уравнение и данные для его оценки содержат наблюдения для разных по качеству объектов: для мужчин и женщин, для белых и черных. вопрос, который нас может здесь заинтересовать, следующий – верно ли, что рассматриваемая модель совпадает для двух выборок, относящихся к объектам разного качества? Ответить на этот вопрос можно при помощи теста Чоу.

Рассмотрим модели:

, i=1,…,N (1);

, i=N+1,…,N+M (2).

В первой выборке N наблюдений, во второй – М наблюдений. Пример: Y – заработная плата, объясняющие переменные – возраст, стаж, уровень образования. Следует ли из имеющихся данных, что модель зависимости заработной платы от объясняющих переменных, стоящих в правой части одинакова для мужчин и женщин?

Н₀:

Для проверки этой гипотезы можно воспользоваться общей схемой проверки гипотез при помощи сравнения регрессии с ограничениями и регрессии без ограничений. Регрессией без ограничений здесь является объединение регрессий (1) и (2), т. е. ESS_UR = ESS₁ + ESS₂, число степеней свободы – N + M - 2k. Регрессией с ограничениями (т. е. регрессией в предположении, что выполнена нулевая гипотеза) будет являться регрессия для всего имеющегося набора наблюдений:

, i = 1,…, N+M (3).

Оценивая (3), получаем ESS_R. Для проверки нулевой гипотезы используем следующую статистику:

, которая в случае справедливости нулевой гипотезы имеет распределение Фишера с числом степеней свободы числителя k и знаменателя N + M - 2k.

Если нулевая гипотеза справедлива, мы можем объединить имеющиеся выборки в одну и оценивать модель для N + M наблюдений. Если же нулевую гипотезу отвергаем, то мы не можем слить две выборки в одну, и нам придется оценивать эти две модели по отдельности.

 

 

Изучение общей линейной модели, рассмотренной нами ранее, весьма существенно, как мы видели, опирается на статистический аппарат. Однако, как и во всех приложениях мат. статистики, сила метода зависит от предположений, лежащих в его основе и необходимых для его применения. Некоторое время мы будем рассматривать ситуации, когда одна или более гипотез, лежащих в основе линейной модели, нарушается. Мы рассмотрим альтернативные методы оценивания в этих случаях. Мы увидим, что роль одних гипотез более существенна по сравнению с ролью других. Нам надо посмотреть, к каким последствиям может привести нарушения тех или иных условий (предположений), уметь проверить, удовлетворяются они или нет и знать, какие статистические методы можно и целесообразно применять, когда не подходит классический метод наименьших квадратов.

1. Связь между переменными линейная и выражается уравнением 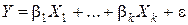- ошибки спецификации модели (невключение в уравнение существенных объясняющих переменных, включение в уравнение лишних переменных, неправильный выбор формы зависимости между переменными);

2. X₁,…,X_k – детерминированные переменные – стохастические регрессоры, линейно независимые – полная мультиколлинеарность;

3. ;

4. - гетероскедастичность;

5. при i ¹ k – автокорреляция ошибок

 

Прежде чем приступать к разговору, рассмотрим следующие понятия: парный коэффициент корреляции и частный коэффициент корреляции.

 

Предположим, что мы исследуем влияние одной переменной на другую переменную (Y и X). Для того чтобы понять, насколько эти переменные связаны между собой, мы вычисляем парный коэффициент корреляции по следующей формуле:

Если мы получили значение коэффициента корреляции близкое к 1, мы делаем вывод о том, что переменные достаточно сильно связаны между собой.

Однако, если коэффициент корреляции между двумя исследуемыми переменными близок к 1, на самом деле они могут и не быть зависимыми. Пример с душевнобольными и радиоприемниками – пример так называемой «ложной корреляции». Высокое значение коэффициента корреляции может быть обусловлено и существованием третьей переменной, которая оказывает сильное влияние на первые две переменные, что и служит причиной их высокой коррелируемости. Поэтому возникает задача расчета «чистой» корреляции между переменными X и Y, т. е. корреляции, в которой исключено влияние (линейное) других переменных. Для этого и вводят понятие коэффициента частной корреляции.

Итак, мы хотим определить коэффициент частной корреляции между переменными X и Y, исключив линейное влияние переменной Z. Для его определения используется следующая процедура:

1. Оцениваем регрессию ,

2. Получаем остатки ,

3. Оцениваем регрессию ,

4. Получаем остатки ,

5. - выборочный коэффициент частной корреляции, измеряет степень связи между переменными X и Y, очищенную от влияния переменной Z.

Прямые вычисления:

Свойство:

Процедура построения коэффициента частной корреляции обобщается на случай, если мы хотим избавиться от влияния двух и более переменных.

 

1. Совершенная мультиколлинеарность.

Одно из требований Гаусса-Маркова говорит нам о том, чтобы объясняющие переменные не были связаны никаким точным соотношением. Если такое соотношение между переменными существует, мы говорим о том, что в модели присутствует совершенная мультиколлинеарность. Пример. Рассмотрим модель со средней оценкой на экзамене, состоящую из трех объясняющих переменных: I - доход родителей, D - среднее число часов, затраченных на обучение в день, W - среднее число часов, затраченных на обучение в неделю. Очевидно, что W=7D. И это соотношение будет выполняться для каждого студента, который попадет в нашу выборку. Случай полной мультиколлинеарности отследить легко, поскольку в этом случае невозможно построить оценки по методу наименьших квадратов.

2. Частичная мультиколлинеарность или просто мультиколлинеарность.

Гораздо чаще встречается ситуация, когда между объясняющими переменными точной линейной зависимости не существует, но между ними существует тесная корреляционная зависимость – этот случай носит название реальной или частичной мультиколлинеарности (просто мультиколлинеарность) – существование тесных статистических связей между переменными. Надо сказать, что вопрос мультиколлинеарности – это вопрос скорее степени выраженности явления, а не его вида. Оценка любой регрессии будет страдать от нее в том или ином виде, если только все независимые переменные не окажутся абсолютно некоррелированными. Рассмотрение данной проблемы начинается только тогда, когда это начинает серьезно влиять на результаты оценки регрессии (наличие статистических связей между регрессорами вовсе не обязательно дает неудовлетворительные оценки). Итак, мультиколлинеарность – это проблема, когда тесная корреляционная зависимость между регрессорами ведет к получению ненадежных оценок регрессии.

 

Последствия мультиколлинеарности:

Формально, поскольку (X'X) – невырожденная, то мы можем построить МНК-оценки коэффициентов регрессии. Однако вспомним, как выражаются теоретические дисперсии оценок коэффициентов регрессии: , где aⁱⁱ - i-й диагональный элемент матрицы . Поскольку матрица (X'X) близка к вырожденной и det(X'X) » 0, то

1) на главной диагонали обратной матрицы стоят очень большие числа, поскольку элементы обратной матрицы обратно пропорциональны det(X'X). Следовательно, теоретическая дисперсия i-го коэффициента достаточно большая и оценка дисперсии так же большая, следовательно, t- статистики небольшие, что может привести к статистической незначимости i-го коэффициента. Т. е. переменная оказывает значимое влияние на объясняемую переменную, а мы делаем вывод о ее незначимости.

2) Поскольку оценки и зависят от (X'X)^-1, элементы которой обратно пропорциональны det(X'X), то если мы добавим или уберем одно-два наблюдения, добавив или убрав, таким образом, одну-две строки к матрице X'X, то значения и могут измениться существенным образом, вплоть до смены знака – неустойчивость результатов оценивания.

3) Трудность интерпретации уравнения регрессии. Допустим, у нас в уравнении есть две переменные, которые связаны между собой между собой: X₁ и X₂. Коэффициент регрессии при X₁ интерпретируется как мера изменения Y за счет изменения X₁ при прочих равных условиях, т.е. значения всех других переменных остаются прежними. Однако, поскольку переменные Х₁ и Х₂ связаны, то изменения в переменной Х₁ повлекут за собой предсказуемые изменения в переменной Х₂ и значение Х₂ не останется прежним.

Пример: , где Х₁ – общая площадь, Х₂ – жилая площадь. Мы говорим: "Если жилая площадь увеличиться на 1 кв. м., то при прочих равных условиях цена квартиры увеличиться на долл". Однако в этом случае и жилая площадь увеличится на 1 кв. м. и прирост цены будет . Разграничить влияние на переменную Y каждой переменной в отдельности уже не представляется возможным. Выход в данной ситуации с ценой на квартиру -–включить в модель не общую площадь, а так называемую "добавочную" или "дополнительную" площадь.

 

Признаки мультиколлинеарности.

Точных критериев для определения наличия (отсутствия) мультиколлинеарности не существует. Однако есть эвристические рекомендации по ее выявлению:

1) Анализируют матрицу парных коэффициентов корреляции между регрессорами и если значение коэффициента корреляции близко к 1, то это считается признаком мультиколлинеарности.

2) Анализ матрицы корреляции – лишь поверхностное суждение о наличии (отсутствии) мультиколлинеарности. Более внимательное изучение этого вопроса достигается при помощи расчета коэффициентов частной корреляции или расчетов коэффициентов детерминации каждой из объясняющих переменных по всем другим объясняющим переменным в регрессии .

3) Можно посчитать определитель матрицы (Х’X) и если он близок к нулю, то это тоже свидетельствует о наличии мультиколлинеарности.

4) (Х’X) – симметричная положительно определенная матрица, следовательно, все ее собственные числа неотрицательны. Если определитель матрицы (Х’X) равен нулю, то минимальное собственное число так же ноль и непрерывность сохраняется. Следовательно, по значению манимального собственного числа можно судить и о близости к нулю определителя матрицы (Х’X). Кроме этого свойства минимальное собственное число важно еще и потому, что стандартная ошибка коэффициента обратно пропорциональна .

5) О наличии мультиколлинеарности можно судить по внешним признакам, являющимся следствиями мультиколлинеарности:

a) некоторые из оценок имеют неправильные с точки зрения экономической теории знаки или неоправданно большие значения;

b) небольшое изменение исходных экономических данных приводит к существенному изменению оценок коэффициентов модели;

c) большинство t-статистик коэффициентов незначимо отличаются от нуля, в то же время модель в целом является значимой, о чем говорит высокое значение F-статистики.

Как избавится от мультиколлинеарности, как ее устранить:

1) Использование факторного анализа. Переход от исходного набора регрессоров, среди которых есть статистически зависимые, к новым регрессорам Z₁,…,Z_m при помощи метода главных компонент – вместо исходных переменных вместо исходных переменных рассматриваем некоторые их линейные комбинации, корреляция между которыми мала или отсутствует вообще. Задача здесь – дать содержательную интерпретацию новым переменным Z. Если не удалось – возвращаемся к исходным переменным, используя обратные преобразования. Полученные оценки будут, правда, смещенными, но будут иметь меньшую дисперсию.

2) Среди всех имеющихся переменных отобрать наиболее существенно влияющих на объясняемую переменную факторов. Процедуры отбора будут рассмотрены ниже.

3) Переход к смещенным методам оценивания.

Когда мы сталкиваемся с проблемой мультиколлинеарности, то у неискушенного исследователя поначалу возникает желание просто исключить лишние регрессоры, которые, возможно, служат ее причиной. Однако не всегда ясно, какие именно переменные являются лишними в указанном смысле. Кроме того, как будет показано ниже, отбрасывание так называемых существенно влияющих переменных приводит к смещенности МНК-оценок.