Коэффициенты эластичности

Рис. 2.1.2. Коореляционные поля для линейной и нелинейной зависимости

После того как определена спецификация модели, необходимо перейти к следующему этап – к оценке параметров выбранной модели. Метод, по которому происходит оценка параметров, зависит от того, какая функциональная зависимость выбрана.

Парная линейная регрессия

Классический подход к оцениванию параметров линейной регрессии основан на методе наименьших квадратов (МНК). МНК позволяет получить такие оценки параметров а и b, при которых сумма квадратов отклонений фактических (статистических, реальных) значений результативного признака у от расчетных (теоретических) будет минимальна.

(2.2)

Для линейной однофакторной модели:

(2.3)

Функция двух переменных S (а,b) может достигнуть экстремума в том случае, когда первые частные производные этой функции равняются нулю, т.е. когда

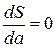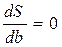и (2.4)

Вычисляя эти частные производные, получим:

(2.5)

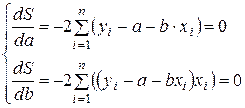
После несложных преобразований получаем систему нормальных уравнений для определения величины параметров а и b уравнения линейной однофакторной модели:

(2.6)

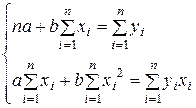
где п – количество наблюдений (объем выборки).

В уравнении регрессии параметр а показывает совокупное влияние на результативный признак неучтенных (не выделенных для исследования) факторов; его вклад в значение результирующего показателя не зависит от изменения факторов; параметр b – коэффициент регрессии – показывает, на сколько изменяется в среднем значение результативного признака при увеличении факторного на единицу собственного измерения.

Полученное уравнение регрессии всегда дополняют показателем тесноты линейной связи – коэффициентом корреляции

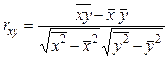(2.7)

Коэффициентом корреляции всегда находится в интервале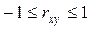

Если 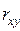→1, то связь между переменными прямая и сильная.

Если 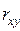→-1, то связь между переменными обратная и сильная.

Если 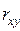→0, то говорят об отсутствие линейной связи между переменными

Параметр b в уравнении регрессии и коэффициент корреляции всегда имеют одинаковый знак.

После того как построено уравнение регрессии, необходимо оценить его качество. Для этого можно использовать коэффициент детерминации 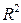и среднюю ошибку аппроксимации .

Коэффициент детерминации рассчитывается по следующей формуле:

(2.8)

Значение коэффициента детерминации всегда находится внутри интервала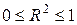

Если →1, то это означает высокое качество построенного уравнения. Такое уравнение можно использовать для прогнозирования и дальнейшего анализа.

Если →0, то это означает плохое качество построенного уравнения. Такое уравнение нельзя использовать для прогнозирования и дальнейшего анализа.

Коэффициент детерминации характеризует долю дисперсии результативного признака у, объясняемую регрессией, в общей дисперсии результативного признака. Чем больше доля объясненной дисперсии, тем меньше роль прочих неучтенных факторов, и следовательно построенная модель хорошо аппроксимирует исходные статистические данные.

Основные причины того, что построенной уравнение регрессии низкого качества:

1. Неправильно выбрана спецификация модели, то есть от линейной модели необходимо перейти к нелинейной.

2. В модели не учтен один из важных объясняющих показателей, то есть от парной регрессии необходимо перейти к множественной.

Средняя ошибка аппроксимации это среднее отклонение расчетных значений от фактических.

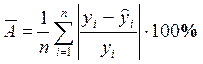(2.9)

Значение 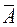до 8%, свидетельствует о хорошем качестве модели

Коэффициент эластичности Э показывает на сколько процентов, в среднем по совокупности, изменится результат у от своей средней величины при изменении фактора х на 1% от своего среднего значения. Расчетная формула для коэффициента эластичности:

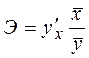(2.10)

В таблице 2.2.1 приведены коэффициенты эластичности для разных функций.

Таблица 2.2.1

Вид функции, у	Первая производная,	Коэффициент эластичности,
Линейная у = а + bx + ε	b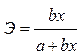
Парабола у = а + bx + cx²+ ε	b + 2cx
Гипербола у = а + + ε
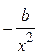
Показательная у = а b^xε	ln b a b^x	Э = х lnb
Степенная у = а х^b ε	a b x^b^-1	Э = b
Экспоненциальная у = е^a⁺^bxε	b е^a+bx	Э = b х

2.3. Предпосылки МНК (условия Маркова-Гаусса)

Для получения по МНК наилучших результатов необходимо чтобы выполнялись следующие условия (предпосылки) относительно случайного отклонения ε.

1. Математическое ожидание случайного отклонения ε_i равно нулю: М(ε_i)=0, для всех наблюдений.

2. Дисперсия случайных отклонений ε_i постоянна D(ε_i)=D(ε_j)=σ² , для любых наблюдений i и j. Постоянство дисперсии называется гомоскедастичностью, непостоянство дисперсии называется гетероскедастичностью.

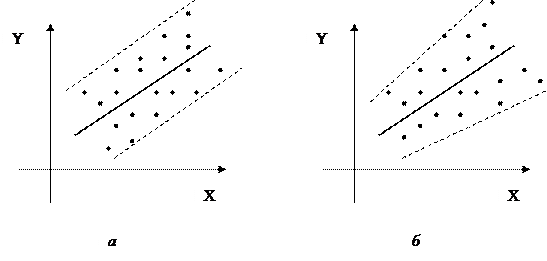
На рис.2.3.1, а показано постоянство дисперсии, на рис. 2.3.1, б показано непостоянство дисперсии

рис.2.3.1 Постоянство и непостоянство дисперсии отклонений

3. Случайные отклонения ε_i и ε_j являются независимыми друг от друга.

4. Случайное отклонение ε_j должно быть независимо от объясняющих переменных.

5. Ошибки ε_i подчиняются нормальному распределению.

F-тест Фишера на состоятельность регрессии

После того как найдено уравнение линейной регрессии, проводится оценка значимости как уравнения в целом, так и отдельных его параметров.

Оценка значимости уравнения регрессии в целом производится с помощью F – критерия Фишера. При этом выдвигается нулевая гипотеза H₀: уравнение регрессии статистически незначимо.

Для этого выполняется сравнение фактического (расчетного) критерия F_р с табличным значением F_табл.Таблицы критических значений составлены на основе двухпараметрического распределения неотрицательной случайной величины (F-распределения Фишера) в зависимости от численных значений степеней свободы v₁ = m и v₂= n - m - 1,при различных уровнях значимости (в приложении 2 дана таблица F-распределения Фишера для трех различных значений уровня значимости 5%, 1%, 0,1%).

(3.7)

Если > F_табл при заданном уровне значимости α, гипотеза H₀ о случайной природе формирования уравнения регрессии отклоняется, то есть уравнение регрессии статистически значимо.

Если <F_табл при заданном уровне значимости α, гипотеза H₀ о случайной природе формирования уравнения регрессии не отклоняется и признается статистическая незначимость и ненадежность уравнения регрессии.

Анализ точности определения параметров регрессии

Для оценки статистической значимости параметров регрессии используют t – критерий Стьюдента. При этом выдвигается нулевая гипотеза H₀ : параметр b (a) статистически незначим (близок к нулю). При отклонении Н₀ параметр b (a) считается статистически значимым, что указывает на наличие определенной линейной зависимости между х и у.

Находится расчетное значение t – критерии для каждого параметра. Для параметра b:

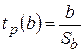(3.8)

для параметра a:

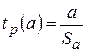(3.9)

Полученные расчетные значения сравниваются с табличным (приложение 1) для заданного уровня значимости α и при ν=n-m-1 степенях свободы.

Если , то гипотеза H₀ о статистической незначимости параметра b отклоняется, то есть параметра b статистически значим.

Если , то гипотеза H₀ о статистической незначимости параметра а отклоняется, то есть параметра а статистически значим.

Если , то гипотеза H₀ о статистической незначимости параметра b принимается.

Если 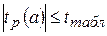, то гипотеза H₀ о статистической незначимости параметра а принимается.

Стандартные ошибки параметров и самой линейной регрессии определяются по формулам:

Стандартная ошибка параметра b:

(3.10)

Стандартная ошибка параметра а:

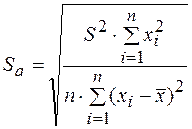(3.11)

Стандартная ошибка регрессии (мера разброса зависимой переменной вокруг линии регрессии):

(3.12)

Проверка выполнимости предпосылок МНК.
Статистика Дарбин-Уотсона

Статистическая значимость параметров регрессии и близкое к единице значение коэффициента детерминации R² не гарантирует высокое качество уравнения регрессии. Поэтому следующим этапом проверки качества уравнения регрессии является определение выполнимости предпосылок МНК. Для этого рассмотрим статистику Дарбина-Уотсона.

Оценивая линейное уравнение регрессии, мы предполагаем, что реальная взаимосвязь переменных линейна, а отклонения от регрессионной прямой являются случайными, независимыми друг от друга величинами с нулевым математическим ожиданием и постоянной дисперсией. Если эти предположения не выполняются, то оценки несмещенности, эффективности, состоятельности и анализ их значимости будут неточными.

На практике для анализа коррелированности отклонений вместо коэффициента корреляции используют тесно с ним связанную статистику Дарбина-Уотсона DW, рассчитываемую по формуле:

(3.13)

Здесь сделано допущение, что при больших n выполняется соотношение:

(3.14)

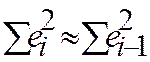
Тогда

(3.15)

Нетрудно заметить, что если 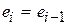, то и DW=0. Если 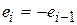, то 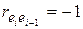и DW=4. Во всех других случаях 0<DW<4.

При случайном поведении отклонений можно предположить, что в одной половине случаев знаки последовательных отклонений совпадают, а в другой – противоположны. Так как абсолютная величина отклонений в среднем предполагается одинаковой, то можно считать, что в половине случаев , а в другой – . Тогда

(3.16)

Таким образом, необходимым условием независимости случайных отклонений является близость к двойке значения статистики Дарбина-Уотсона. Тогда, если DW≈2, мы считаем отклонения от регрессии случайными (хотя они в действительности могут и не быть таковыми). Это означает, что построенная линейная регрессия, вероятно, отражает реальную зависимость.

Возникает вопрос, какие значения DW можно считать статистически близкими к двум?

Для ответа на этот вопрос разработаны специальные таблицы критических точек статистики Дарбина-Уотсона (Приложение 3), позволяющие при данном числе наблюдений п, количестве объясняющих переменных т и заданном уровне значимости α определять границы приемлемости (критические точки) наблюдаемой статистики DW.

Для заданных α, п, т в таблице (Приложение 3) указываются два числа: d₁ – нижняя граница и d_u – верхняя граница. Для проверки гипотезы об отсутствии автокорреляции остатков используется числовой отрезок, изображенный на рис. 3.6.1.

Выводы осуществляются по следующей схеме.

Если DW < d₁, то это свидетельствует о положительной автокорреляции остатков.

Если DW > 4 – d₁, то это свидетельствует об отрицательной автокорреляции остатков.

При d_u < DW < 4 – d_u гипотеза об отсутствии автокорреляции остатков принимается.

Если d₁ < DW < d_u или 4 – d_u < DW < 4 – d₁, то гипотеза об отсутствии автокорреляции не может быть ни принята, ни отклонена.

Модели парной нелинейной регрессии

Во многих практических случаях моделирование экономических зависимостей линейными уравнениями дает вполне удовлетворительный результат и не может использоваться для анализа и прогнозирования. В силу многообразия и сложности экономических процессов ограничиться рассмотрением лишь линейных регрессионных моделей невозможно. Многие экономические зависимости не являются линейными по своей сути, и поэтому их моделирование линейными уравнениями регрессии не даст положительного результата. Например, при рассмотрении спроса у на некоторый товар от цены х данного товара в ряде случаев можно ограничиться линейным уравнением регрессии: у=а+bx, но данная модель справедлива не всегда: при эластичном спросе скорее подойдет гиперболическая модель у=а+b∙1/x. При анализе издержек у от объема выпуска х наиболее обоснованной является полиномиальная (точнее, кубическая) модель.

При рассмотрении производственных функций линейная модель является нереалистичной. В этом случае обычно используются степенные модели. Например, широкую известность имеет производственная функция Кобба-Дугласа (здесь у – объем выпуска; K и L – затарты капитала и труда соответственно; А, α и β – параметры модели).

Различают два класса нелинейных регрессий:

· регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам;

· регрессии, нелинейные по оцениваемым параметрам.

Примером нелинейной регрессии по включаемым в нее объясняющим переменным могут служить следующие функции:

– полиномы разных степеней: y = a + b₁ x + b₂ x² + e,

y = a + b₁ x + b₂ x² + b₃ х³ + e;

– равносторонняя гипербола: у = а + 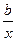+ ε.

К нелинейным регрессиям по оцениваемым параметрам относятся функции:

– степенная: у = а х^b ε;

– показательная: у = а b^xε;

– экспоненциальная: у = е^a⁺^bx ε.

Нелинейность по переменным устраняется путем замены переменной. Например, нелинейное уравнение 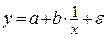после замены переменной становится линейным: .

Нелинейность по параметру часто устраняется путем логарифмического преобразования уравнения. Например, нелинейные уравнения после логарифмирования сводятся к линейным степенная функция 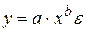после логарифмирования становится линейной: ;

Нелинейные однофакторные регрессионные модели. Линеаризация

Что же необходимо сделать, если исследователь пришел к выводу, что анализируемая зависимость нелинейная? В этой ситуации существует два основных варианта действий:

-вначале стоит попытаться подобрать такое преобразование к анализируемым переменным, которое позволило бы представить существующую нелинейную зависимость в виде линейной функции. Этот процесс называется линеаризацией;

-если линеаризация невозможна, то тогда к исследуемой зависимости необходимо применять методы нелинейной регрессии. Рассмотрение этих методов выходит за рамки данного курса.

Если процесс линеаризации возможен, то после его проведения к вновь введенным переменным можно применить МНК.