Основные этапы регрессионного анализа
К основным этапам эконометрического исследования можно отнести следующие:
1. Постановка проблемы
На данном этапе выбирают ряд экономических показателей, зависимость между которыми нужно выявить и исследовать.
2. Сбор и анализ статистических данных
На данном этапе по выбранным ранее показателям собирают статистические данные. Сбор статистических данных может происходить либо методом опросов, анкетирования, либо используя официальную статистическую информацию, то есть статистические сборники, которые выходят ежегодно.
3. Построение эконометрической модели.
На данном этапе необходимо представить экономическую модель в математической форме, удобной для дальнейшего анализа. Этот этап называют этапом спецификации модели.
4. Оценка параметров модели
На данном этапе необходимо по отдельным методам количественно определить параметры выбранной модели, делающих эту модель наиболее адекватной к реальным статистическим данным, которые были получены на втором этапе исследования.
5. Проверка качества построенной модели и найденных параметров
На данном этапе по определенным критериям необходимо доказать, что построенная модель и найденные параметры надлежащего качества. Если построенная модель или найденные параметры низкого качества необходимо указать основные причины, по которым была получена модель низкого качества.
6. Использование построенной модели в экономических исследованиях
На данном этапе полученную модель необходимо уметь использовать для объяснения поведения исследуемых показателей, осмысленного проведения экономической политики и построения прогноза.
Между двумя показателями X и Y можно указать два вида взаимосвязей.
1. Оба показателя являются равнозначными, то есть не подразделяются на зависимый и независимый (цена на товар и объем спроса на этот товар). Основным в этом случае является вопрос о наличии и силе взаимосвязи. Для анализа таких показателей зачастую используют корреляционный анализ.
2. Один из показателей выделяется как независимый (объясняющий) Х, а другой как независимый (объясняемый) Y (среднемесячный доход и потребление продуктов питания). В данном случае изменение первого из них влечет изменение второго. Для анализа таких показателей используют корреляционно-регрессионный анализ.
В чем же разница между корреляцией и регрессией? На первый взгляд может показаться, что понятие регрессии сходно с понятием корреляции, так как в обоих случаях речь идет о статистической взаимосвязи между переменными. Однако между ними есть существенные различия.
Корреляция ничего не говорит о причинной зависимости между переменными, то есть если наличие корреляции между переменными Х и Y, этот факт не подразумевает того, что изменения значений Х обуславливают изменения значений Y, или наоборот. Корреляция всего лишь констатирует факт того, что изменения одной переменной в среднем соотносятся с изменениями другой.
Однако в случае регрессионного анализа подразумевается именно причинная взаимосвязь, то есть изменения одной переменной происходят вследствие изменений другой.
Регрессия – функциональная зависимость между объясняющими переменными и условным математическим ожиданием зависимой переменной, которая строится с целью прогнозирования среднего значения зависимой переменной, при фиксированных значениях первых.
(2.1)
у – зависимая переменная (результативный признак)
х1, х2,…,хm – объясняющие переменные (независимые)
ε – случайные отклонения
Причины присутствия в моделях случайных отклонений:
1. Не включение в модель всех объясняющих переменных
2. Неправильный выбор функциональной формы в модели
3. Агрегирование переменных
4. Ошибки измерения
5. Ограниченность статистических данных
6. Непредсказуемость человеческого фактора.
В зависимости от числа объясняющих переменных регрессия подразделяется на парную (однофакторная) и множественную, по типу связи – на линейную и нелинейную. Виды регрессионных связей можно увидеть на рис. 2.1.1.
В случае парной регрессии вид зависимости между переменными можно выбрать с помощью изображения корреляционного поля. Корреляционное поле – графическое изображение статистических данных на плоскости. По расположению точек на корреляционном поле выдвигают предположение о виде функциональной зависимости между переменными.
На рис.2.1.2, а взаимосвязь между переменными близка к линейной функции. На рис.2.1.2, б взаимосвязь между переменными, скорее всего, описывается квадратичной функцией.
 |
|
|
Рис. 2.1.2. Коореляционные поля для линейной и нелинейной зависимости
После того как определена спецификация модели, необходимо перейти к следующему этап – к оценке параметров выбранной модели. Метод, по которому происходит оценка параметров, зависит от того, какая функциональная зависимость выбрана.
Парная линейная регрессия
Классический подход к оцениванию параметров линейной регрессии основан на методе наименьших квадратов (МНК). МНК позволяет получить такие оценки параметров а и b, при которых сумма квадратов отклонений фактических (статистических, реальных) значений результативного признака у от расчетных (теоретических)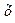 
будет минимальна.
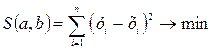(2.2)
Для линейной однофакторной модели:
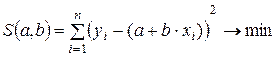(2.3)
Функция двух переменных S (а,b) может достигнуть экстремума в том случае, когда первые частные производные этой функции равняются нулю, т.е. когда
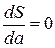и 
(2.4)
Вычисляя эти частные производные, получим:
|
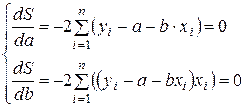
После несложных преобразований получаем систему нормальных уравнений для определения величины параметров а и b уравнения линейной однофакторной модели:
|
где п – количество наблюдений (объем выборки).
В уравнении регрессии параметр а показывает совокупное влияние на результативный признак неучтенных (не выделенных для исследования) факторов; его вклад в значение результирующего показателя не зависит от изменения факторов; параметр b – коэффициент регрессии – показывает, на сколько изменяется в среднем значение результативного признака при увеличении факторного на единицу собственного измерения.
Полученное уравнение регрессии всегда дополняют показателем тесноты линейной связи – коэффициентом корреляции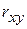 
(2.7)
Коэффициентом корреляции всегда находится в интервале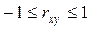 
Если 
→1, то связь между переменными прямая и сильная.
Если →-1, то связь между переменными обратная и сильная.
Если →0, то говорят об отсутствие линейной связи между переменными
Параметр b в уравнении регрессии и коэффициент корреляции 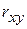всегда имеют одинаковый знак.
После того как построено уравнение регрессии, необходимо оценить его качество. Для этого можно использовать коэффициент детерминации 
и среднюю ошибку аппроксимации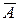 
.
Коэффициент детерминации рассчитывается по следующей формуле:
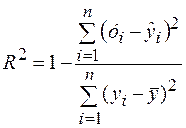(2.8)
Значение коэффициента детерминации всегда находится внутри интервала 
Если 
→1, то это означает высокое качество построенного уравнения. Такое уравнение можно использовать для прогнозирования и дальнейшего анализа.
Если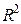 
→0, то это означает плохое качество построенного уравнения. Такое уравнение нельзя использовать для прогнозирования и дальнейшего анализа.
Коэффициент детерминации характеризует долю дисперсии результативного признака у, объясняемую регрессией, в общей дисперсии результативного признака. Чем больше доля объясненной дисперсии, тем меньше роль прочих неучтенных факторов, и следовательно построенная модель хорошо аппроксимирует исходные статистические данные.
Основные причины того, что построенной уравнение регрессии низкого качества:
1. Неправильно выбрана спецификация модели, то есть от линейной модели необходимо перейти к нелинейной.
2. В модели не учтен один из важных объясняющих показателей, то есть от парной регрессии необходимо перейти к множественной.
Средняя ошибка аппроксимации это среднее отклонение расчетных значений от фактических.
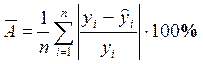(2.9)
Значение 
до 8%, свидетельствует о хорошем качестве модели
Коэффициент эластичности Э показывает на сколько процентов, в среднем по совокупности, изменится результат у от своей средней величины при изменении фактора х на 1% от своего среднего значения. Расчетная формула для коэффициента эластичности:
(2.10)
В таблице 2.2.1 приведены коэффициенты эластичности для разных функций.
Таблица 2.2.1