Исследование влияния факторов на изменение результирующего показателя в уравнении регрессии.

Процесс построения мат. модели:

1) закл. в выборе вида мат. уравнения и определения параметров этого уравнения;

выбор вида затруднен т.к., набор этих уравнений бесконечен, но в большинстве случаев для описания модели можно аппроксимировать в виде:

y=a0 +b1x1 +b2x2…+bpxp (1)

Данный подход правомерен, если действительно подход имеет устойчивую прямолин. тенденцию изменения.

Если мы изучаем процесс на ограниченном диапазоне изменения факториального признака и на этом диапазоне реальный процесс может быть аппроксимирован прямой линией.

Доказано, что 1 повышает порядок уравнения (1) можно подобрать такое уравнение, что у теоретическое в точности совпадет с у фактическим во всех точках наблюдения. Но практическая ценность такого уравнения очень мала, т.к. она выявляет не закономерность развития изучаемого процесса, появляющееся на фоне случайных колебаний, а сами это сл. Колеб. Теоретически, найден. Уранение регрессии имеет вид:

(2) 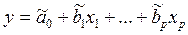, где а0, b1, bp – оценки истинных значений параметров.

Нахождением уравнения (2) решается основная задача теории корреляции, кот. Закл. в том, чтобы на основе наблюд., над большим количеством данных, выяснить как в среднем изменяется ф-я у при изменении части факториальных признаков, которые включены в модель. Полагается что осн. факториальные пр-ли явл. Неизменными.

2)задача теории корреляции закл в том, чтобы определить силу с которой найденная зависимость проявляется среди нарушающих ее воздействий т.е. необх определить:

а)как, насколько значительно включенные в модель факторы влияют на результирующий показатель в целом;

б) определить насколько значительно влияет каждый фактор на результативный показатель.

Дан задачи решаются путем вычисления коэффициентов множественной корреляции, коэф. Парной корреляции и коэф. Частной корреляции.

Определение значений этих коэф. Основано на законе сложения дисперсий, кот. Справедлив. Для ф-ий линейно зависящих от параметров:

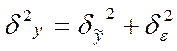
, где

общая дисперсия;дисперсия теоретических значений; 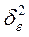остаточная дияперсия.

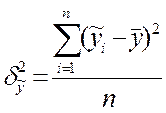
Отношение дисперсии теоретических значений у к общей дисперсии называется коэф множ. Детерминац.:

где Rквадрат показывает долю изменения у,кот. Можно объяснить изменением включенных в модель факторов.

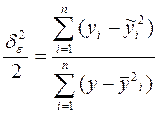коэф сходимости = доля изменения у кот можно объяснить действием не включенных в модель факторов.

R=- показ насколько тесна линейно-статистическая связь между Утеор и Хфактич.

Если R=0 то эта связь отсутствует

Для функции нелинейно-зависящих от параметров закон сложения дисперсий не действует.

Другим показателем, характеризующим силу влияния отдельн факториального на величину у явл коэф парной корреляции

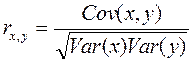где Cov (x,y) =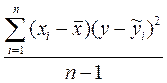

Var(x)=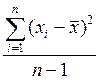

Недостатком дан коэф явл то, что он правильно отражает силу влияния ф-ра Х на У при условии, если остальные ф-ры, в интервале наблюдения, неизменны.

Для выявления влияния только одного ф-ра на величину Уиспользуют коэф частной корреляции:, где

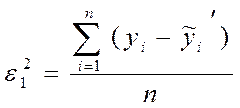
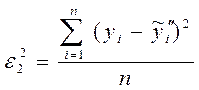
ρх,у характеризует силу влиянт яфактора на Х1.