Проверка соответствия распределения случайной компоненты нормальному закону распределения

Проверка случайности колебаний уровня остаточной последовательности.

Оценка адекватности и точности регрессионных моделей. Общие положения.

В не зависимости от способа нахождения экономико – математических моделей, с использованием статистических данных вопрос об её использовании для анализа и прогнозирования экономических явлений может быть положительно решен только после установления адекватности этой модели , т.е. соответствия к исследованному юбъекту или явлению.

Матем.модели – абстактные конструкции и они никогда не могут быть полностью адекватны, исследуемыми, поэтому при исследовании адекватности имеют ввиду соответствие модели наиболее важным (для исследователя) свойством изучаемого объекта или явления.

При представлении инфо в виде ряда чисел, то модель, этого ряда чисел считается адекватной, если она правильно отражает систематические компоненты этого числового ряда. Систематического компоненты= T_i-трендовую составляющую;

S_i- Сезонную составляющую;

C_i- циклическую составляющую;

y=T_i+S_i+C_i+e_i;

Методы: 1) серии, основанные на медиане выбора;

_~

ei=yi+yi ei= теоритические остатки;

0,5;-0,5;-1,5;2;-2,3;-0,6

Этапы: 1) упорядоч. порядки по возрастанию -1,5;-0,6;-0,5;2;2,3;

2)срединные значения этого ряда 0,5

3)медиану сравниваем с e фактическим: «+» - > медианы e₀ «-» - меньше медианы e₀ 0;-;+;+;-; n_ф=3(серии)

Серии К_мф=2

При 5% значимости нулевой гипотезы проверяется как отношение К_мф<[3,3 * log(n+1)]

n-число наблюдений nф>[1/2(n+1-1.96)]

Если выполн. 2. неравенство, то выборка считается случайной более 95%. И нулевая гипотеза отвергается. Выборка получается неслучайной.

Данная проверка производится обычно приближенно с помощью нахождения показателей ассиметрии γ₁ и эксцесса γ₂. Это производится на основании сравнения найденных показателей с теоретическими. При нормальном распределении некоторой генеральной совокупности показатели ассиметрии и эксцесса должны быть равны нулю (γ₁=0, γ₂ =0). При конечной выборке из генеральной совокупности показатели ассиметрии и эксцесса имеют отклонения от нуля.

Для оценки соответствия выбранной совокупности данных нормальному закону распределения используется так называемая оценка показателей эксцесса и ассиметрии.

В качестве оценки асимметрии используется формула:

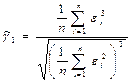
Оценка эксцесса:

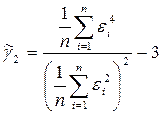
Здесь и - соответственно выборочные характеристики ассиметрии и эксцесса, а и 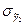- их допустимые среднеквадратичные ошибки, ε_i - остаточная компонента.

Если одновременно выполняются неравенства для 5% уровня значимости 0^ой гипотезы:

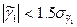
то считается, что фактическая кривая распределения допустимо близка к кривой нормального распределения.

Если:

то с вероятностью более 5% можно утверждать, что фактическая кривая распределения недопустимо отклоняется от кривой нормального распределения.

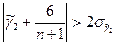
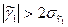
Следовательно, адекватности нет.

Другие случаи требуют дополнительной проверки при помощи более сложных критериев.