Парная линейная регрессия: Статистический анализ модели

Лекция 4

Элементы статистического анализа модели
Проверка статистической значимости параметров уравнения регрессии
Анализ дисперсии
Проверка общего качества уравнения регрессии
F-статистика. Распределение Фишера в регрессионном анализе.

-1-

Оценивая зависимость между эндогенными и экзогенными переменными (y и x) по выборочным данным не всегда удается на первом этапе получить удачную модель регрессии. При этом каждый раз следует оценивать качество полученной модели. Качество модели оценивается по 2м направлениям:

· Содержательная оценка качества модели

· Статистическая оценка качества модели

Содержательный анализ подразумевает анализ экономического смысла модели. Действительно ли оказались важными те факторы которые значимы в эконом теории и т.д.

Статистический анализ модели включает следующие элементы:

Проверку статистической значимости параметров уравнения регрессии
Проверку общего качества уравнения регрессии
Проверку свойств данных, выполнение которых предполагалось при оценивании уравнения

-2-

Статистическая значимость параметров уравнения регрессии определяется по t-статистике или статистике Стьюдента. Так:

tb – t-статистика для коэффициента регрессии b

mb – стандартная ошибка коэффициента регрессии.

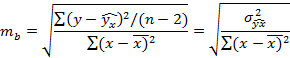
Так же рассчитывают t-статистику для коэффициентов корреляции R:

Таким образом tb^2=t_r^2=F. То есть проверка статистической значимости коэффициента регрессии b равносильна проверке статистической значимости коэффициента корреляции

Коэффициент корреляции показывает тесноту корреляционной связи(между х и у).

Для линейной регрессии коэффициент корреляции:

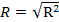
Для определения тесноты связи используют обычно таблицу Чеглока

R 0,1 – 0,3 слабая

R 0,3 – 0,5 умеренная

R 0,5-,07 заметная

R 0,7-0,9 высокая

R 0,9 до 0,99 весьма высокая связь между х и у

Коэффициент корреляции -1<R<1

Часто для практических целей рассчитывают коэффициент эластичности, бета-коэффициент:

Эластичностью функции у=f(x) называется предел отношения относительных переменных у и х

Эластичность показывает на сколько %-в изменится у при изменении х на 1 %.

Для парной линейной регрессии коэффициент эластичности вычисляется по формуле:

Он показывает на сколько %-в изменится у в среднем при изменении х в среднем на 1 %.

Бетта-коэффициент равен:

– среднее квадрат отклонение x

– Среднее квадрат отклонение у

Бетта-коэффициент показывает на какую величину от своего среднего квадратического отклонения изменится у при изменении х на величину своего среднего квадратического отклонения.

=3=

Анализ дисперсии

В анализе дисперсии особое место занимает разложение общей суммы квадратов отклонений переменой у от у среднего на две части: на сумму объясненную регрессией и сумму, не объясненную регрессией.

Общая сумма квадратов отклонений равна сумме квадратов отклонений объясненной регрессией плюс остаточной сумме квадратов отклонений.

Эти суммы связаны с числом степеней свободы df – это число свободы независимого варьирования признаков.

Так общая сумма квадратов отклонений имеет общее число степеней свободы (n – 1).

Сумма квадратов отклонений объясненная регрессией имеет степень свободы 1, так как переменная зависит от одной величины – коэффициента регрессии b.

Между числом степеней свободы существует равенство, из которого:

N – 1 = 1 + n – 2

Разделим каждую сумму на соответствующее число степеней свободы, получим средний квадрат отклонений или дисперсию:

D_общ = D_факт + D _ост

=4=

Оценить общее качество уравнения регрессии означает, установить соответствует ли математическая модель, выражающая зависимость между переменными экспериментальным данным и достаточно ли включенных в модель переменных, объясняющих у.

Оценить общие качества модели = оценить надежность модели = оценить достоверность уравнения регрессии.

Оценка общего качества модели регрессии осуществляется на основе дисперсионного анализа. Для оценки качества модели рассчитывают коэффициент детерминации:

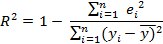
В числителе выборочная оценка остаточной дисперсии, в знаменателе выборочная оценка общей дисперсии.

Коэффициент детерминации характеризует долю вариации зависимой переменной, объясненной с помощью уравнения регрессии.

Так, если R квадрат равен 0,97 это значит что на 97% изменений у обусловлено изменением х.

Чем ближе R квадрат к единице, тем сильнее статистически значимая линейная связь между х и у.

Для получения не смещенных оценок дисперсии( коэффициента детерминации) и числитель, и знаменатель в формуле делят на соответствующее число степеней свободы:

=5=

Для определения статистической значимости коэффициента детерминации R квадрат проверяется нулевая гипотеза для F-статистики , рассчитываемой по формуле:

Для парной линейной:

F-расчетная сравнивается со значением статистики в таблице. F-табличная рассматривается с числом степеней свободы m, n-m-1, при уровне значимости альфа.

Если F расч> F табл то нулевая гипотеза отвергается, принимается гипотеза о статистической значимости коэффициента детерминации R квадрат.

F-критерий Фишера = факторная дисперсия / на остаточную дисперсию:

Лекция №5

Проверка свойств данных, выполнение которых предполагалось при оценивании уравнения регрессии

1. Автокорреляция в остатках

2. Статистика Дарбина-Уотсона

3. Примеры

=1=

При оценивании параметров модели регрессии предполагается, что отклонении

обладает следующими свойствами:

1. 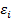носят случайный характер

2. Математическое ожидание равно нулю M(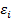) =0

3. Дисперсия этих отклонений одинакова D(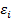)^2 = D(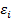)^2=

4. 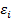независимы между собой

В таком случае оценки параметров регрессии полученные с помощью метода наименьших квадратов обладают 3-мя важными свойствами:

1. Несмещенность

2. Состоятельностью

3. Эффективностью

Предполагаемые свойства на самом деле могут не выполняться, тогда полученные оценки параметров регрессии a и b не будут обладать указанными характеристиками.

В каком случае отклонения могут не обладать этими свойствами:

1. В случае, если взаимосвязь между х и у не линейна.

2. Связь между переменными х и у линейна, но на исследуемый показатель воздействует фактор, не включенный в модель. Величина такого фактора может менять свою динамику за рассматриваемый период. Особенно это характерно для лаговых переменных.

Обе причины свидетельствуют о том, что полученное уравнение регрессии можно улучшить, оценив нелинейную зависимость или добавив в исходную модель дополнительный фактор.

Четвертая предпосылка метода наименьших квадратов говорит о том, что отклонения 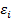являются независимыми между собой, однако при исследовании и анализе исходных данных на практике встречаются ситуации, когда эти отклонения содержат тенденцию или циклические колебания.

Например:

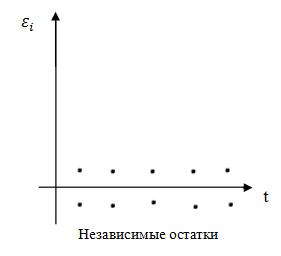
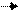
Проявление тенденции или циклических колебаний свойственно временным рядам.

Присутствие тенденций или циклов в остатках представляет собой автокорреляцию остатков.

Автокорреляция – это зависимость каждого следующего значения остатков от значения предшествующих.

Автокорреляция свидетельствует о том, что на последующие наблюдения наибольшее воздействие оказывает результат предшествующих наблюдений.

Обычно проверяется коррелированность или некоррелированность не любых значений остатков, а двух соседних.

Соседними величинами остатков являются последовательные во времени остатки ( во временных рядах) или последовательные по возрастанию х (в пространственной выборке).

Рассмотрим временной ряд последовательных значений курса ценной бумаги, наблюдаемых в моменты времени от 1 до 100.

Из рисунка видно, что курс акции растет. На результаты последующих торгов оказывает влияние результат предшествующих торгов: если в какой-то момент курс акций завышен, то он будет завышен и в следующий момент. Если в какой-то момент курс акций будет занижен, то он будет занижен и в следующий момент. Это называется положительной автокорреляцией.

На графике положительная автокорреляция выражается в чередовании зон, которые находятся выше уравнения регрессии и зон ниже уравнения регрессии.

Реже встречается на практике отрицательная автокорреляция, например, при работе с полугодовыми данными показателя с сезонным характером.

Графически отрицательная корреляция проявляется в том, что результаты наблюдений часто пересекают график уравнения регрессии.

При отрицательной автокорреляции наблюдения действуют друг на друга по принципу маятника, т.е. завышение значения в предшествующем наблюдении приводит к занижению результата в последующем и наоборот.

(4)

Таким образом, отсутствие корреляции между соседними величинами остатков есть основание того, что корреляция отсутствует в целом в остатках, тогда оценки параметров регрессии, полученные с помощью МНК дают адекватные и эффективные результаты.

Для соседних величин остатков можно рассчитать коэффициент автокорреляции остатков первого порядка:

=2=

На практике используют тесно связанную с этим коэффициентом статику Дар-Уотсона

Критерий (тест) DW определяет наличие автокорреляции между соседними величинами остатков. Он основан на простой идее: если корреляция ошибок регрессии не равна нулю, то она присутствует и в остатках регрессии ei, получаемых методом МНК.