Пример решения задачи
ØЗадача 3
В результате наблюдений пары случайных величин 
и 
получены данные, которые представлены в виде табл. 13
Таблица 13
|
|
|
|
|
|
|
|
| -291 | -219 | -241 | -240 | ||||
| -270 | -281 | -243 | -277 | ||||
| -279 | -262 | -245 | -279 | ||||
| -282 | -302 | -282 | -253 | ||||
| -254 | -275 | -252 | -275 | ||||
| -264 | -267 | -276 | -248 | ||||
| -216 | -290 | -276 | -243 | ||||
| -276 | -266 | -246 | -264 | ||||
| -248 | -270 | -284 | -267 | ||||
| -253 | -283 | -271 | -213 | ||||
| -276 | -237 | -227 | -218 | ||||
| -262 | -222 | -256 | -223 | ||||
| -234 | -281 | -309 | -278 | ||||
| -243 | -269 | -300 | -236 | ||||
| -313 | -257 | -310 | -263 | ||||
| -278 | -235 | -255 | -268 | ||||
| -292 | -275 | -252 | -243 | ||||
| -271 | -276 | -274 | -271 | ||||
| -256 | -282 | -291 | |||||
| -291 | -277 | -264 |
Требуется:
1) построить корреляционную таблицу;
2) построить корреляционное поле;
3) построить уравнение регрессии на ;
4) вычислить выборочный коэффициент корреляции 
;
5) сделать вывод о связи переменных и .
Решение
Задачу решаем с помощью электронного процессора MS Excel.
Алгоритм
Шаг 1. Внесём данные в таблицу, состоящую из двух столбцов, не забудьте в первой строке внести обозначения столбцов, в нашем случае это будут и .
Шаг 2. Для каждой из переменных и найдём наибольшее и наименьшее значения, используя статистические функции МИН и МАКС: 
, 
;
, 
.
Шаг 3. Найдём размах для каждой из переменных 
и : 
и 
соответственно:
;
.
Шаг 4. Положим число интервалов для переменной равно 6, число интервалов для переменной равно 7. Как правило, число интервалов для каждой из переменных берут в пределах от 5 до 11. Критерием выбора числа интервалов служит требование: вариационный ряд не должен быть большим (формула Стерджеса), следовательно, и корреляционная таблица будет обозримой.
Шаг 5. Найдём шаги 
, 
для переменных и . В нашем случае
; 
.
Шаг 6. Для каждой из переменных и найдём начальные значения 
, 
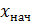первых интервалов, и конечные значения 
, 
последних интервалов.
Начальные значения вычисляем как
, 
.
Для конечных значений , последних интервалов для переменных и должны выполняться условия:
, 
.
Границы промежуточных интервалов получаем, следуя правилу:
, 
, 
.
Для переменной в нашем случае будем иметь:
.
Округляем до целых значений: 
.
Границы интервалов: 
; 
.
Проверяем выполнение условия, наложенного на конечное значение последнего интервала для переменной :
.
Итак, интервалы для переменной : 
).
Для переменной в нашем случае будем иметь:
.
Округляем до целых значений: 
.
Границы интервалов:
; 
.
Проверяем выполнение условия, наложенного на конечное значение последнего интервала для переменной :
.
Интервалы для переменной :
,
.
Шаг 7. Скопируем данные на новое место и выполним сортировку данных в порядке возрастания по первому столбцу. Данные в таком виде потребуются для заполнения корреляционной таблицы, а именно для вычисления чисел 
.
Шаг 8. Построим интервалы для каждой из переменных и , вычислим число значений и , попадающих на каждый из интервалов:
| Интервалы
| 
| Интервалы 
| 
|
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
|
Значения 
можно использовать для контроля правильности заполнения корреляционной таблицы.
Шаг 9. Построим корреляционную таблицу:
| (53; 58] | (58; 63] | (63; 68] | (68; 73] | (73; 78] | (78; 83) | |
| (-321; -304] | ||||||
| (-304; -287] | ||||||
| (-287; -270] | ||||||
| (-270; -253] | ||||||
| (-253; -236] | ||||||
| (-236; -219] | ||||||
| (-219; -202) |
Используем полученные ранее значения , чтобы убедиться в том, что корреляционная таблица построена верно, объём выборки 
, по столбцам:
;
по строкам:
.
Шаг 10. Найдём середины интервалов для переменной :
| Интервалы
| (53; 58] | (58; 63] | (63; 68] | (68; 73] | (73; 78] | (78; 83) |
| Середины интервалов | 55,5 | 60,5 | 65,5 | 70,5 | 75,5 | 80,5 |
Найдём середины интервалов для переменной :
| Интервалы
| (-321; -304] | (-304; -287] | (-287; -270] | (-270; -253] |
| Середины интервалов | -312,5 | -295,5 | -278,5 | -261,5 |
| Интервалы
| (-253; -236] | (-236; -219] | (-219; -202) |
| Середины интервалов | -244,5 | -227,5 | 210,5 |
Найдём условные средние 
:
|
| -213,90 | -235,06 | -252,15 | -273,86 | -293,38 | -312,50 |
Построим вспомогательную таблицу (табл.14), которая будет основой для построения поля корреляции.
Таблица 14
|
| 
| 
| 
| 
| 
| 
| 
|
|
| 55,5 | -227,5 | -210,5 | -213,90 | |||||
| 60,5 | -244,5 | -227,5 | -237,06 | |||||
| 65,5 | -261,5 | -244,5 | -252,15 | |||||
| 70,5 | -278,5 | -261,5 | -273,86 | |||||
| 75,5 | -295,5 | -278,5 | -293,38 | |||||
| 80,5 | -312,5 | -312,50 |
Построим корреляционное поле (рис. 7).
Рис. 7. Поле корреляции
Шаг 11. Подготовим новую таблицу для вычисления коэффициентов системы линейных уравнений (2) относительно 
. Все вычисления приведены в табл. 15.
Þ Примечание. Следует заметить, что все данные предыдущего шага надо брать из табл. 15.
Шаг 12. Запишем уравнение регрессии на 
. В нашем случае это будет уравнение
.
Анализируя данное уравнение, можно сказать, что имеем отрицательную (обратную) корреляцию, поскольку коэффициент регрессии 
.
Шаг 13. Вычислим выборочный коэффициент корреляции (4): 
. Согласно шкале Чеддока связь между переменными величинами и весьма высокая, согласно шкале Голубкова - сильная.
Шаг 14. Для построения уравнения регрессии сформируем дополнительную табл. 16, содержащую:
- средние значения 
переменной ,
- средние значения 
переменной (обозначим 
),
- значения переменной , вычисленные на основании уравнения регрессии (обозначим 
),
- разность между экспериментальным и теоретическим значениями переменной 
: 
, а также 
для получения оценки метода наименьших квадратов (МНК) [4].
Таблица 15
| Y\X | (53; 58] | (58; 63] | (63; 68] | (68; 73] | (73; 78] | (78; 83) | ||||||||
| ycp\xcp | 55,5 | 60,5 | 65,5 | 70,5 | 75,5 | 80,5 | 
| 
| 
| 
| 
| |||
| (-321;-304] | -312,5 | -937,5 | 241,5 | -75468,75 | 292968,75 | |||||||||
| (-304;-287] | -295,5 | -2068,5 | 528,5 | -156171,75 | 611241,75 | |||||||||
| (-287;-270] | -278,5 | -6962,5 | 1767,5 | -492248,75 | 1939056,25 | |||||||||
| (-270;-253] | -261,5 | -4707,0 | 1224,0 | -320076,00 | 1230880,50 | |||||||||
| (-253;-236] | -244,5 | -3667,5 | 962,5 | -235331,25 | 896703,75 | |||||||||
| (-236;-219] | -227,5 | -1365,0 | 358,0 | -81445,00 | 310537,50 | |||||||||
| (-219;-202) | -210,5 | -842,0 | 222,0 | -46731,00 | 177241,00 | |||||||||
| -20550,0 | -1407472,50 | 5458629,50 | |||||||||||
| 277,50 | 544,50 | 1310,00 | 2326,50 | 604,00 | 241,50 | 5304,00 | |||||||
| 15401,25 | 32942,25 | 85805,00 | 164018,25 | 45602,00 | 19440,75 |  =
| 6,46 | ||||||
| -1069,50 | -2115,50 | -5043,00 | -9037,50 | -2347,00 | -937,50 |  =
| -3,97 | ||||||
| -213,90 | -235,06 | -252,15 | -273,86 | -293,38 | -312,50 | ||||||||
| Уравнение регрессии Y на X: y=6,46-3,97*x | ||||||||||||||
Коэффициенты системы относительно , 
|  =
| |||||||||||||
| 78,0 | 5304,0 | -20550,0 |  =
| |||||||||||
| 5304,0 | 363209,5 | -1407472,5 |  =
| -785655 | Дисп.х: | 32,5 | Ср_кв_откл для х: | 5,7 | ||||||
| Дисп.y: | 570,4 | Ср_кв_откл для y: | 23,9 | |||||||||||
Из полученной таблицы выпишем коэффициенты системы (2): 
Решая систему (2), получаем коэффициенты уравнения регрессии 
, 
.
Таблица 16
| 
|
| 
|
|
| 55,5 | -213,90 | -213,88 | -0,0250 | 0,0006 |
| 60,5 | -235,06 | -233,73 | -1,3350 | 1,7822 |
| 65,5 | -252,15 | -253,58 | 1,4250 | 2,0306 |
| 70,5 | -273,86 | -273,43 | -0,4350 | 0,1892 |
| 75,5 | -293,38 | -293,28 | -0,1050 | 0,0110 |
| 80,5 | -312,50 | -313,13 | 0,6250 | 0,3906 |
| 4,40 |
Шаг 15. На основании сформированной табл.16 построим уравнение регрессии на (рис. 7).
Рис. 7. Уравнение регрессии и условные средние значения
G Вывод. Между переменными и установлена сильная обратная корреляция, уравнение регрессии на : 
, выборочный коэффициент корреляции 
. Из табл. 16 можно увидеть, что 
[4].
Варианты заданий
В результате наблюдений пары случайных величин и получены данные, которые представлены в виде таблицы.
Требуется:
1) построить корреляционную таблицу;
2) построить корреляционное поле;
3) построить уравнение регрессии на ;
4) вычислить выборочный коэффициент корреляции ;
5) сделать вывод о связи переменных и .
Вариант 0
Таблица 0
|
|
|
|
|
|
|
|
|
.
PВариант 1
Таблица 1
|
|
|
|
|
|
|
|
|
| -201 | -237 | -226 | -279 | ||||
| -199 | -209 | -218 | -259 | ||||
| -206 | -243 | -245 | -251 | ||||
| -221 | -239 | -247 | -207 | ||||
| -238 | -221 | -201 | -257 | ||||
| -256 | -238 | -215 | -227 | ||||
| -222 | -238 | -209 | -214 | ||||
| -230 | -223 | -212 | -243 | ||||
| -234 | -207 | -203 | -214 | ||||
| -217 | -237 | -252 | -196 | ||||
| -253 | -216 | -251 | -239 | ||||
| -228 | -228 | -206 | -210 | ||||
| -230 | -193 | -214 | -221 | ||||
| -201 | -234 | -227 | |||||
| -237 | -229 | -269 |
.
PВариант 2
Таблица 2
|
|
|
|
|
|
|
|
|
.
PВариант 3
Таблица 3
|
|
|
|
|
|
|
|
|
.
PВариант 4
Таблица 4
|
|
|
|
|
|
|
|
|
.
PВариант 5
Таблица 5
|
|
|
|
|
|
|
|
|
| -37 | -32 | -34 | -38 | ||||
| -36 | -30 | -29 | -30 | ||||
| -32 | -35 | -38 | -31 | ||||
| -30 | -34 | -30 | -32 | ||||
| -32 | -29 | -33 | -31 | ||||
| -33 | -35 | -30 | -38 | ||||
| -27 | -34 | -39 | -32 | ||||
| -28 | -30 | -25 | -32 | ||||
| -40 | -35 | -32 | -28 | ||||
| -33 | -30 | -35 | -34 | ||||
| -31 | -35 | -30 | -29 | ||||
| -31 | -36 | -34 | -35 | ||||
| -39 | -33 | -33 | -32 | ||||
| -30 | -24 | -31 | -30 | ||||
| -34 | -29 | -34 | -29 | ||||
| -37 | -32 | -29 | -31 |
.
PВариант 6
Таблица 6
|
|
|
|
|
|
|
|
|
| -262 | -256 | -273 | -270 | ||||
| -261 | -288 | -270 | -264 | ||||
| -268 | -269 | -266 | -269 | ||||
| -255 | -276 | -264 | -268 | ||||
| -261 | -266 | -270 | -262 | ||||
| -275 | -248 | -285 | -280 | ||||
| -263 | -281 | -268 | -263 | ||||
| -279 | -266 | -268 | -289 | ||||
| -269 | -282 | -272 | -278 | ||||
| -276 | -281 | -269 | -279 | ||||
| -274 | -265 | -273 | -265 | ||||
| -272 | -288 | -283 | -273 | ||||
| -284 | -290 | -269 | -283 | ||||
| -276 | -278 | -284 | -252 | ||||
| -275 | -282 | -270 | -283 | ||||
| -276 | -276 | -271 | -285 | ||||
| -250 | -271 | -271 | -279 | ||||
| -278 | -279 | -289 | -264 | ||||
| -268 | -273 | -294 | -270 | ||||
| -288 | -271 | -271 | -281 | ||||
| -266 | -264 | -271 | -268 | ||||
| -275 | -270 | -279 | -277 | ||||
| -285 | -261 | -277 | -273 | ||||
| -259 |
.
PВариант 7
Таблица 7
|
|
|
|
|
|
|
|
|
.
PВариант 8
Таблица 8
|
|
|
|
|
|
|
|
|
.
PВариант 9
Таблица 9