Корреляция и регрессия
Для описания, анализа и прогнозирования явлений и процессов в экономике, технике, природных явлениях, социальной жизни, т. е во всех сферах жизнедеятельности человека, применяют математические модели в форме уравнений или функций. Математические модели исследуемого объекта, отражая его основные свойства и абстрагируясь от второстепенных, позволяют судить о его поведении в определённых условиях.
Одной из основных задач математической статистики является исследование зависимости между двумя или несколькими переменными.
В нашем случае ограничимся изучением линейной связи между двумя случайными величинами  и
и  .
.
Две переменные  и
и  могут быть независимыми либо связанными функциональной или статистической зависимостью. Строгая функциональная зависимость реализуется редко, поскольку хотя бы одна из переменных подвержена случайным факторам.
могут быть независимыми либо связанными функциональной или статистической зависимостью. Строгая функциональная зависимость реализуется редко, поскольку хотя бы одна из переменных подвержена случайным факторам.
ÆСтатистической зависимостью называется такая зависимость, при которой изменение одной из величин влечёт за собой изменение распределения другой.
Если при изменении одной из величин изменяется среднее значение другой, то в этом случае статистическая зависимость является корреляционной [3].
Æ Корреляционной зависимостью между двумя переменными величинами называется функциональная зависимость между значениями одной из них и условным математическим ожиданием другой.
Основная цель изучения зависимостей между случайными величинами заключается в прогнозировании с данной вероятностью области значений одной случайной величины на основании наблюдаемых значений другой случайной величины [1], [3].
На практике при исследовании зависимости между случайными величинами  и
и  часто ограничиваются исследованием зависимости между
часто ограничиваются исследованием зависимости между  и условным математическим ожиданием
и условным математическим ожиданием  .
.
Æ Функция  называется функцией регрессии первого рода
называется функцией регрессии первого рода  на
на  (
(  по
по  ), а её график - линией регрессии
), а её график - линией регрессии  на
на  (
(  по
по  ) [3] .
) [3] .
Аналогично функцию  называют функцией регрессии
называют функцией регрессии  на
на  (
(  по
по  ).
).
Þ Примечание. Часто функцию регрессии  на
на  обозначают
обозначают
 ,
,  ,
,  ,
,
 или
или  .
.
Такому обозначению легко найти объяснение, поскольку оценкой (несмещённой, состоятельной и эффективной) математического ожидания  случайной величины
случайной величины  является средняя величина, которая обозначается
является средняя величина, которая обозначается  .
.
Уравнение регрессии  делает возможным точечные предсказания значений условных математических ожиданий составляющих
делает возможным точечные предсказания значений условных математических ожиданий составляющих  двумерной случайной величины
двумерной случайной величины  по значению составляющей
по значению составляющей  . Однако для такого прогноза необходимо знать закон распределения двумерной случайной величины
. Однако для такого прогноза необходимо знать закон распределения двумерной случайной величины 
 , который на практике, как правило, неизвестен.
, который на практике, как правило, неизвестен.
По этой причине исследование зависимости случайной величины от ряда неслучайных и случайных величин приводит к моделям регрессии на базе выборочных данных. В качестве оценок математических ожиданий принимаются условные средние, которые находятся по данным выборки  , объёма
, объёма 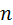 .
.
Условным средним  называется среднее арифметическое наблюдавшихся значений
называется среднее арифметическое наблюдавшихся значений  , соответствующих значению
, соответствующих значению  . Например, при
. Например, при  величина
величина  принимает значения
принимает значения
 ,
,
тогда  .
.
Ситуация может быть такой: при фиксированном значении переменной  , пусть это будет опять
, пусть это будет опять  (в данном случае это значение не играет роли) случайная величина принимает значения 1, 3, 3, 4, 5, 2, 3, 1, 4, 4, 5, 2, 3, 2. На основании этих данных делаем вывод, что количество наблюдений равно 14. Говорим, что объём выборки равен 14 и пишем
(в данном случае это значение не играет роли) случайная величина принимает значения 1, 3, 3, 4, 5, 2, 3, 1, 4, 4, 5, 2, 3, 2. На основании этих данных делаем вывод, что количество наблюдений равно 14. Говорим, что объём выборки равен 14 и пишем  . При вычислении среднего значения
. При вычислении среднего значения  вместо непосредственной суммы значений
вместо непосредственной суммы значений 

построим таблицу, где в первой строке перечислим значения переменной  , во второй – сколько раз эти значения повторились в данном эксперименте.
, во второй – сколько раз эти значения повторились в данном эксперименте.
Это замечание важно для понимания правила заполнения корреляционной таблицы, о которой речь пойдёт ниже по тексту.

| |||||
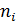
|
Тогда условное среднее значение величины  находим как
находим как
 .
.
Þ Примечание. Условным средним  называется среднее арифметическое наблюдавшихся значений
называется среднее арифметическое наблюдавшихся значений  , соответствующих
, соответствующих  .
.
Результаты выборки  пары случайных величин
пары случайных величин  представим в виде табл. 6, которая называется корреляционной таблицей.
представим в виде табл. 6, которая называется корреляционной таблицей.
Таблица 6
 
| 
| … | 
| 
|

| 
| … | 
| 
|
| … | … | |||

| 
| … | 
| 
|

| 
| … | 
| 
|
Þ Примечание. Числа  в корреляционной таблице указывают на то, сколько раз пара
в корреляционной таблице указывают на то, сколько раз пара  встретилась среди наблюдаемых значений случайных величин
встретилась среди наблюдаемых значений случайных величин  .
.
Æ Если результаты выборки пары случайных величин  представить в виде точек
представить в виде точек  (
(  ) в декартовой системе координат, то получим точечную диаграмму, называемой корреляционным полем.
) в декартовой системе координат, то получим точечную диаграмму, называемой корреляционным полем.
?Упражнение 5. В результате эксперимента получены значения двух величин  . Данные приведены в табл. 7.
. Данные приведены в табл. 7.
Таблица 7

| ||||||||||||||||||||

|
1) постройте корреляционную таблицу,
2) найдите условные средние  ,
,
3) постройте:
- корреляционное поле,
- ломаную, соединяющую условные средние  .
.
Решение
По приведённым данным видим, что количество наблюдений равно двадцати, т. е. объем выборки  . Сгруппируем данные табл. 6 в виде корреляционной таблицы (табл. 7) и найдём условные средние
. Сгруппируем данные табл. 6 в виде корреляционной таблицы (табл. 7) и найдём условные средние  .
.
Таблица 7
 
| 
| |||||

| ||||||

| ||||||

| 
| 
| 
| 
| 
|
Сформируем новую таблицу (табл. 8), удобную для построения точечной диаграммы в MS Excel для точек  (
( 
 ) и условных средних
) и условных средних  . Заметим, что матрица будет транспонированной.
. Заметим, что матрица будет транспонированной.
Таблица 8
 
| 
| 
| 
| 
|
| 1,25 | ||||
| 2,60 | ||||
| 1,67 | ||||
| 2,25 | ||||
| 1,50 |
Внесём изменения в предыдущую таблицу, проставив значения  , соответствующие значениям
, соответствующие значениям 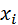 (
( 
 ). Полученную таблицу (табл. 9) используем для построения корреляционного поля (рис. 5)
). Полученную таблицу (табл. 9) используем для построения корреляционного поля (рис. 5)
Таблица 9


| 
| 
| 
| 
|
| 1,25 | ||||
| 2,60 | ||||
| 1,67 | ||||
| 2,25 | ||||
| 1,50 |
Заметим, что точки, соответствующие условным средним значениям  (в нашем случае – это 1.25, 2.60, 1.67, 2.25, 1.50) для наглядности соединили ломаной линией. На диаграмме условные средние
(в нашем случае – это 1.25, 2.60, 1.67, 2.25, 1.50) для наглядности соединили ломаной линией. На диаграмме условные средние  в легенде обозначены как
в легенде обозначены как  .
.

Рис. 5. Корреляционное поле
Æ Оценку функции регрессии называют эмпирической регрессией, или функцией регрессии второго рода [3].
Поскольку функции регрессии обладают свойством минимальности, т. е. среднее квадратическое отклонение случайной величины  от функции
от функции  является наименьшим, то для нахождения эмпирических уравнений регрессии
является наименьшим, то для нахождения эмпирических уравнений регрессии  применяется метод наименьших квадратов (МНК) [4].
применяется метод наименьших квадратов (МНК) [4].
Регрессионный анализ – это анализ функций регрессии первого и второго рода. Перед проведением регрессионного анализа необходимо по статическим данным выбрать общий вид эмпирической функции регрессии.
На практике часто полагают, что функция регрессии – это линейная функция  .
.
Коэффициент  называют коэффициентом регрессии
называют коэффициентом регрессии  на
на  .
.
Будем искать функцию регрессии 
 на
на  в самом простом виде - линейном:
в самом простом виде - линейном:
 . (1)
. (1)
Коэффициенты  этого уравнения неизвестны. Для определения их используем МНК. Результатом этого метода будем иметь систему линейных уравнений относительно неизвестных коэффициентов
этого уравнения неизвестны. Для определения их используем МНК. Результатом этого метода будем иметь систему линейных уравнений относительно неизвестных коэффициентов  :
:
 (2)
(2)
Коэффициенты  находим по формулам Крамера (3):
находим по формулам Крамера (3):
 . (3)
. (3)
Здесь
 ,
,
 ,
,
 .
.
Как оценить меру связи случайных величин  и
и  ?
?
В измерении этой связи участвует коэффициент ковариации  :
:
 .
.
Этот коэффициент может принимать значения на всей числовой прямой, поэтому не вполне пригоден для измерения степени зависимости. В этом смысле более пригоден нормированный коэффициент ковариации, или коэффициент корреляции  ,
,
 , здесь
, здесь  ;
;  .
.
Þ Примечания:
1) для независимых случайных величин  и
и  коэффициент корреляции равен нулю:
коэффициент корреляции равен нулю:  ;
;
2) для линейно связанных случайных величин  и
и  абсолютная величина коэффициента корреляции равна единице:
абсолютная величина коэффициента корреляции равна единице:  ;
;
3) в остальных случаях  ;
;
4) чем ближе  к единице, тем с большим основанием можно считать, что случайные величины
к единице, тем с большим основанием можно считать, что случайные величины  и
и  находятся в линейной зависимости;
находятся в линейной зависимости;
5) если  , то это не всегда означает независимость случайных величин. В этом случае говорят, что случайные величины некоррелированны;
, то это не всегда означает независимость случайных величин. В этом случае говорят, что случайные величины некоррелированны;
6) из независимости случайных величин вытекает некоррелированность, но наоборот – не всегда.
Оценкой коэффициента корреляции  служит выборочный коэффициент корреляции
служит выборочный коэффициент корреляции  , который можно вычислить по формулам
, который можно вычислить по формулам
 или
или  , (4) здесь
, (4) здесь
 ,
,  ,
,  .
.
Þ Примечание. Коэффициент  присутствует в вычислении коэффициента корреляции
присутствует в вычислении коэффициента корреляции  . Это ещё одна формула, которую можно применять для вычисления выборочного коэффициента корреляции
. Это ещё одна формула, которую можно применять для вычисления выборочного коэффициента корреляции  .
.
G Вывод. Проверка гипотезы «функция регрессиипредставлена линейным уравнением  » осуществляется посредством корреляционного анализа.
» осуществляется посредством корреляционного анализа.
Корреляционный анализ – это анализ оценки коэффициента корреляции. Этот анализ позволяет ответить на вопрос, существует ли линейная функциональная зависимость между случайными величинами  и
и  , и позволяет измерить степень близости статистической зависимости к функциональной.
, и позволяет измерить степень близости статистической зависимости к функциональной.
Если установлено, что зависимость между некоторыми наблюдаемыми величинами  и
и  существует, то на практике важно знать, какая она: сильная или слабая (
существует, то на практике важно знать, какая она: сильная или слабая (  близок к 1 или нет), положительная (прямая) или отрицательная (обратная) (
близок к 1 или нет), положительная (прямая) или отрицательная (обратная) (  или
или  соответственно). Характер связи и её интерпретация приведены в табл.10.
соответственно). Характер связи и её интерпретация приведены в табл.10.
Таблица 10
| Значение r | Характер связи | Интерпретация связи |

| Отсутствует | Изменение  не влияет на изменения не влияет на изменения 
|

| Прямая | С увеличением  увеличивается увеличивается 
|

| Обратная | С увеличением  уменьшается уменьшается  и наоборот и наоборот
|

| Функциональная | Каждому значению факторного признака строго соответствует одно значение результативного |
Исследуя выборочный коэффициент корреляции, качественную оценку тесноты связи  и
и  можно дать, если воспользоваться шкалой американского учёного-статиста Чеддока (табл. 11) или шкалой Голубкова Е. П., академика Международной академии информатизации (табл. 12).
можно дать, если воспользоваться шкалой американского учёного-статиста Чеддока (табл. 11) или шкалой Голубкова Е. П., академика Международной академии информатизации (табл. 12).
Таблица 11
Шкала Чеддока для оценки корреляции
| № п/п | Критическое значение
коэффициента 
| Показатель связи |
| 0,1 – 0,3 | Слабая корреляционная связь | |
| 0,3 – 0,5 | Умеренная корреляционная связь | |
| 0,5 – 0,7 | Заметная корреляционная связь | |
| 0,7 – 0,9 | Высокая корреляционная связь | |
| 0,9 – 1,0 | Весьма высокая корреляционная связь |
Таблица 12
Шкала Голубкова Е. П. для оценки корреляции
Критическое значение коэффициента 
| Интерпретация |
| 0,00 – 0,20 | Отсутствует |
| 0,21 – 0,40 | Очень слабая |
| 0,41 – 0,60 | Слабая |
| 0,61 – 0,80 | Умеренная |
| 0,81 – 1,00 | Сильная |
Þ Примечание. Некоторые авторы положительную корреляцию называют прямой: с ростом  переменная
переменная  растёт, отрицательную корреляцию – обратной: с ростом
растёт, отрицательную корреляцию – обратной: с ростом  переменная
переменная  убывает и наоборот.
убывает и наоборот.
На графике прямая и обратная корреляция может быть представлена как на рис. 6.


Рис.6. Прямая и обратная корреляции
L Можно ли судить о том, имеем прямую или обратную корреляцию, зная коэффициенты  линейного уравнения регрессии (1)? Достаточно ли одного коэффициента для объяснения этого факта? Если «да», то какого коэффициента? Объясните этот факт по рис. 6.
линейного уравнения регрессии (1)? Достаточно ли одного коэффициента для объяснения этого факта? Если «да», то какого коэффициента? Объясните этот факт по рис. 6.