Примеры решения задач
ØЗадача 1
Анализируетсявыборка из 100 малых предприятий региона. Цель обследования - измерение коэффициента соотношения заёмных и собственных средств на каждом предприятии. Результаты представлены в виде табл. 1.
Таблица 1
Коэффициенты соотношений заёмных и собственных средств на предприятиях
| 5.56 | 5.45 | 5.48 | 5.45 | 5.39 | 5.37 | 5.46 | 5.59 | 5.61 | 5.31 |
| 5.46 | 5.61 | 5.11 | 5.41 | 5.31 | 5.57 | 5.33 | 5.11 | 5.54 | 5.43 |
| 5.34 | 5.53 | 5.46 | 5.41 | 5.48 | 5.39 | 5.11 | 5.42 | 5.48 | 5.49 |
| 5.36 | 5.40 | 5.45 | 5.49 | 5.68 | 5.51 | 5.50 | 5.68 | 5.21 | 5.38 |
| 5.58 | 5.47 | 5.46 | 5.19 | 5.60 | 5.63 | 5.48 | 5.27 | 5.22 | 5.37 |
| 5.33 | 5.49 | 5.50 | 5.54 | 5.40 | 5.58 | 5.42 | 5.29 | 5.05 | 5.79 |
| 5.79 | 5.65 | 5.70 | 5.71 | 5.85 | 5.44 | 5.47 | 5.48 | 5.47 | 5.55 |
| 5.67 | 5.71 | 5.73 | 5.05 | 5.35 | 5.72 | 5.49 | 5.61 | 5.57 | 5.69 |
| 5.54 | 5.39 | 5.32 | 5.21 | 5.73 | 5.59 | 5.38 | 5.25 | 5.26 | 5.81 |
| 5.27 | 5.64 | 5.20 | 5.23 | 5.33 | 5.37 | 5.24 | 5.55 | 5.60 | 5.51 |
Используя полученные данные, выполните следующие задания:
Задание 1. Постройте статистический ряд.
Задание 2. Вычислите относительные частоты, накопленные относительные частоты, плотности относительных частот.
Задание 3. Представьте графически статистический ряд в виде полигона или гистограммы.
Задание 4. Постройте график накопленных относительных частот.
Задание 5. Запишите эмпирическую функцию распределения.
Задание 6. Вычислите точечные оценки параметров закона распределения:
1) выборочное среднее;
2) выборочную дисперсию (смещённую, т. е. неисправленную, и несмещённую, т. е. исправленную);
3) выборочное среднее квадратическое отклонение (смещённое и несмещённое);
4) выборочную моду;
5) выборочную медиану.
Задание 7. Полагая, что данная генеральная совокупность подчиняется нормальному закону, найдите доверительный интервал для неизвестного математического ожидания при условии, что дисперсия неизвестна, если доверительная вероятность задаётся формулой
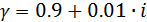, где 
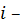последняя цифра шифра зачётной книжки.
Решение
Задание 1. Постройте статистический ряд.
Шаг 1. Внесём данные выборки в MS Excel, упорядочим их по возрастанию, найдём наименьшее и наибольшее значения вариант 
. Это 
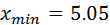и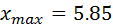 
соответственно. Вычислим размах выборк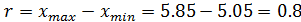и 
и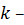 
число интервалов, на которые разбивается диапазон [ 
; 
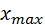], по формулеСтерджеса: 
, 
. Определим длину интервала 
.
Шаг 2. Построим статистический ряд (табл. 2).
Таблица 2
| Интервал | [5.0;5.1) | [5.1;5.2) | [5.2;5.3) | [5.3;5.4) | [5.4;5.5) | [5.5;5.6) | [5.6;5.7) | [5.7;5.8) | [5.8;5.9) |
Частота
|
Þ Примечание. При построении интервалов начальное значение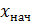 
первого интервала, как правило, надо вычислять по формуле 
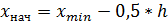, конечное значение 
последнего интервала должно удовлетворять условию 
.
В данном примере частоты первого и последнего интервалов меньше пяти (2 и 2 соответственно). Поэтому объединим первый интервал со вторым, а последний интервал - с предпоследним. Соответственно изменятся и частоты объединённых интервалов (табл. 3).
Таблица 3
| Интервал | [5.0;5.2) | [5.2;5.3) | [5.3;5.4) | [5.4;5.5) | [5.5;5.6) | [5.6;5.7) | [5.7;5.9) |
Частота
|
Задание 2. Вычислите относительные частоты, накопленные относительные частоты, плотности относительных частот.
Построим группированный ряд наблюдений, найдём середины интервалов, вычислим относительные и накопленные относительные частоты, а также плотности относительных частот (табл. 4). Обратите внимание, что длина первого и последнего интервалов равна 0,2.
Таблица 4
| Номер интервала | Интервал | Середина
интервала
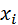
| Частота
| Относительная частота
| Накоплен-ная относительная
частота
| 
|
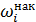
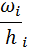
| [5.0; 5.2) | 5.1 | 0.06 | 0.06 | 0.3 | ||
| [5.2; 5.3) | 5.25 | 0.11 | 0.17 | 1.1 | ||
| [5.3; 5.4) | 5.35 | 0.17 | 0.34 | 1.7 | ||
| [5.4; 5.5) | 5.45 | 0.27 | 0.61 | 2.7 | ||
| [5.5; 5.6) | 5.55 | 0.17 | 0.78 | 1.7 | ||
| [5.6; 5.7) | 5.65 | 0.12 | 0.90 | 1.2 | ||
| [5.7; 5.9) | 5.8 | 0.10 | 1.00 | 0.5 |
Задание 3. Представьте графически статистический ряд в виде полигона или гистограммы.
Поскольку исследуем статистический ряд для непрерывной случайной величины, выполним построение гистограммы относительных частот (рис. 1). В роли значения функции, описанной в легенде, выступает плотность относительной частоты.
Рис.1. Гистограмма относительных частот
Задание 4. Постройте график накопленных относительных частот.
Используем вычисленные накопленные частоты, полученные на предыдущем шаге, и построим график накопленных относительных частот (рис. 2).
Рис. 2. График накопленных относительных частот
Задание 5. Запишите эмпирическую функцию распределения.
Эмпирическую функцию распределения записываем, используя вычисленные накопленные относительные частоты:
Задание 6. Вычислите точечные оценки параметров закона распределения:
1) выборочное среднее;
2) выборочную дисперсию (смещённую и несмещённую;
3) выборочное среднее квадратическое отклонение (смещённое и несмещённое);
4) выборочную моду;
5) выборочную медиану.
Þ Примечание. Выполняя данное задание, используйте формулы:
1) выборочное среднее 
2) выборочная смещённая (неисправленная) дисперсия
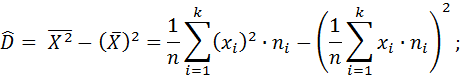
3) выборочная несмещённая (исправленная) дисперсия:
;
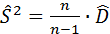4) смещённое выборочное среднее квадратическое отклонение:
;
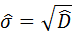5) несмещённое выборочное среднее квадратическое отклонение: 
6) Мода 
и медиана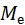 
: 
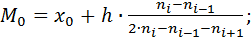
или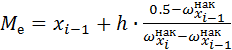 
.
Для решения этой задачи выполним дополнительные вычисления, используя MS Excel.
Задание 7. Полагая, что данная генеральная совокупность подчиняется нормальному закону, найдите доверительный интервал для неизвестного математического ожидания при условии, что дисперсия неизвестна, если доверительная вероятность задаётся формулой 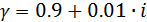, где 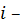последняя цифра шифра зачётной книжки.
Положим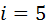 
, тогда доверительная вероятность задана как 
.
Используем ранее полученные выборочное среднее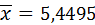 
и исправленное среднее квадратическое отклонение 
.
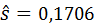По условию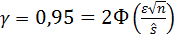 
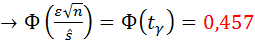. По таблице значений функции Лапласа (прил. 2) находим значение аргумента 
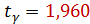. Объём выборки 
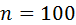. Тогда 
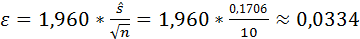. Таким образом, интервал 
покрывает неизвестный параметр такой, как математическое ожидание 
, с надёжностью 
.
Þ Примечание. Если в таблице значений функции Лапласа нет точного значения 
, то следует взять среднее арифметическое двух ближайших соседних значений, одно меньшее , другое - большее .
ØЗадача 2
Выполнены экологические статистические исследования за определённый промежуток времени, например, несанкционированный подъезд машин к закрытой территории мусорных отходов. Получили выборку, данные которой приведены в табл. 5.
Таблица 5
Несанкционированный подъезд машин
По приведённым данным выполните следующие задания:
Задание 1. Постройте статистический ряд.
Задание 2. Вычислите относительные частоты и накопленные относительные частоты.
Задание 3. Представьте графически статистический ряд в виде полигона или гистограммы.
Задание 4. Постройте график накопленных относительных частот.
Задание 5. Запишите эмпирическую функцию распределения.
Задание 6. Вычислите точечные оценки параметров закона распределения:
1) выборочное среднее;
2) выборочную дисперсию (смещённую и несмещённую, или, как её ещё называют, исправленную);
3) выборочное среднее квадратическое отклонение (смещённое и несмещённое);
4) выборочную моду;
5) выборочную медиану.
Задание 7. Положим, изучаемая генеральная совокупность подчиняется нормальному закону распределения. Найдите доверительный интервал для неизвестного математического ожидания при условии, что дисперсия неизвестна и доверительная вероятность задаётся формулой 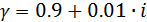, где 
- последняя цифра шифра зачётной книжки.
Решение
Задание 1. Постройте статистический ряд.
Внесём данные выборки в MS Excel, упорядочим их по возрастанию, найдём наименьшее 
и наибольшее 
значения вариант 
Объём выборки 
. Вычислим размах выборки 
. Размах довольно мал, поэтому составим вариационный ряд по значениям, вычислим частоты.
|
| ||||||||
|
|
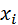
Задание 2. Вычислите относительные частоты и накопленные относительные частоты.
Организуем новую таблицу, вычисления проведём в MS Excel, округляя до двух знаков после десятичной точки. Заметим, что накопленные относительные частоты используем при выполнении задания 4 при записи эмпирической функции распределения. В таблице отметим наибольшую частоту (24) и накопленную относительную частоту 
, которые будут участвовать при нахождении моды и медианы.
Варианта
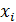
| Частота
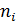
| Относительная частота
| Накопленная относительная частота
|
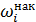
| 0,05 | 0,05 | ||
| 0,16 | 0,22 | ||
| 0,18 | 0,39 | ||
| 0,30 | 0,70 | ||
| 0,20 | 0,90 | ||
| 0,04 | 0,94 | ||
| 0,04 | 0,97 | ||
| 0,03 | 1,00 | ||
| Объём выборки: |
Задание 3. Представьте графически статистический ряд в виде полигона или гистограммы.
Поскольку исследуем статистический ряд для дискретной случайной величины, то построим полигон относительных частот (рис. 3).
Рис.3. Полигон относительных частот
Задание 4. Постройте график накопленных относительных частот.
Искомый график представлен на рис. 4
Рис. 4. График накопленных относительных частот
Задание 5. Запишите эмпирическую функцию распределения.
Запишем эмпирическую функцию распределения, используя данные накопленных относительных частот:
Задание 6. Вычислите точечные оценки параметров закона распределения:
1) выборочное среднее;
2) выборочную дисперсию (смещённую и несмещённую);
3) выборочное среднее квадратическое отклонение (смещённое и несмещённое);
4) выборочные моду и медиану.
Организуем новую таблицу, вычисления выполним в MS Excel.
| Варианта
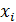
| Частота
| 
| 
| |||
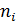
| Объём выборки: | ||||||
| Выборочное среднее: | 2,84 | 10,41 | ||||
| Смещённая выборочная дисперсия: | 2,37 | |||||
| Несмещённая выборочная дисперсия: | 2,40 | |||||
| Выборочное среднее квадратическое отклонение (смещённое): | 1,54 | |||||
| Выборочное среднее квадратическое отклонение (несмещённое): | 1,55 | |||||
| Мода (наибольшая частота 24): | ||||||
| Медиана (элемент, стоящий на 40 - м месте, т. е. серединный элемент): | ||||||
Задание 7. Положим, изучаемая генеральная совокупность подчиняется нормальному закону распределения. Найдите доверительный интервал для неизвестного математического ожидания при условии, что дисперсия неизвестна и доверительная вероятность задаётся формулой 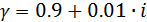, где 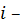последняя цифра шифра зачётной книжки.
Предположим 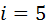, тогда доверительная вероятность вычисляется как 
. Из таблицы, приведённой выше, выборочное среднее 
и исправленное среднее квадратическое отклонение 
.
По условию 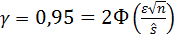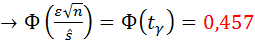. По таблице значений функции Лапласа (прил. 2) находим значение аргумента 
. Объём выборки .
Вычислим 
: 
.
Таким образом, доверительный интервал, покрывающий неизвестное математическое ожидание 
с надёжностью 
, есть 
.
Варианты заданий
! В задачах по данным своего варианта выполните следующие задания:
Задание 1. Постройте статистический ряд.
Задание 2. Вычислите относительные частоты и накопленные относительные частоты.
Задание 3. Представьте графически статистический ряд в виде полигона или гистограммы.
Задание 4. Постройте график накопленных относительных частот.
Задание 5. Запишите эмпирическую функцию распределения.
Задание 6. Вычислите точечные оценки параметров закона распределения:
1) выборочное среднее;
2) выборочную дисперсию (смещённую и несмещённую);
3) выборочное среднее квадратическое отклонение (смещённое и несмещённое);
4) выборочную моду;
5) выборочную медиану.
Задание 7. Положим, изучаемая генеральная совокупность подчиняется нормальному закону распределения. Найдите доверительный интервал для неизвестного математического ожидания при условии, что дисперсия неизвестна и доверительная вероятность задаётся формулой 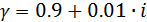, где 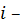последняя цифра шифра зачётной книжки.
PВариант 0
В автопарке проводилось исследование продолжительности автомобильных рейсов (сутки). Результаты дорожной ведомости приведены в табл. 0.
Таблица 0
PВариант 1
В течение квартала на фондовой бирже выполнен сбор данных по количеству сделок для 100 инвесторов. Результаты представлены в виде табл. 1.
Таблица 1
|
| |||||||||||
|
|
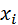
Здесь 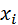- количество сделок, 
- число инвесторов.
PВариант 2
Для изучения распределения заработной платы работников некоторой отрасли за определённый промежуток времени обследовано 100 человек. Результаты представлены в табл. 2.
Таблица 2
| 2.0 | 3.2 | 5.2 | 4.8 | 3.8 | 2.8 | 4.9 | 3.2 | 3.9 | 1.8 |
| 3.7 | 3.2 | 4.5 | 2.5 | 2.3 | 3.4 | 1.1 | 5.7 | 3.3 | 2.7 |
| 2.5 | 1.4 | 2.1 | 3.9 | 2.2 | 1.2 | 4.2 | 5.4 | 2.3 | 4.1 |
| 3.8 | 3.2 | 6.1 | 2.1 | 3.8 | 2.5 | 1.7 | 2.9 | 5.9 | 7.1 |
| 3.9 | 4.2 | 5.8 | 1.8 | 4.2 | 6.1 | 5.1 | 3.3 | 4.2 | 3.6 |
| 3.0 | 2.3 | 1.5 | 3.3 | 3.7 | 2.4 | 1.6 | 2.7 | 4.2 | 5.9 |
| 4.7 | 5.4 | 3.2 | 2.7 | 1.8 | 2.5 | 3.7 | 4.8 | 5.8 | 6.6 |
| 2.8 | 5.4 | 3.2 | 1.6 | 4.7 | 3.3 | 4.9 | 5.3 | 5.1 | 3.2 |
| 1.2 | 2.4 | 6.2 | 7.4 | 7.7 | 6.9 | 7.1 | 8.2 | 6.3 | 5.3 |
| 2.2 | 5.7 | 4.3 | 5.1 | 4.9 | 2.3 | 1.4 | 7.7 | 6.1 | 5.1 |
PВариант 3
Проведено исследование посещаемости интернет-сайта. Несколько часов подряд регистрируется число посетителей, посетивших сайт в течение данного часа. Результаты исследования приведены в табл. 3.
Таблица 3
|
| |||||||
|
| |||||||
|
| |||||||
|
|
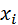
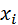
Здесь 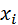- число посетителей, - время (ч).
PВариант 4
В течение трёх месяцев проводились измерения барометрического давления воздуха (мм рт. ст.). Результаты приведены в табл. 4.
Таблица 4
|
| ||||||||||
|
| ||||||||||
|
| ||||||||||
|
|
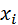
PВариант 5
Проведено исследование продолжительности работы лампочек (ч/10). Результаты исследования приведены в таб. 5.
Таблица 5
PВариант 6
На некотором участке дороги проведены измерения скорости автомобилей, км/ч. Результаты измерения даны в табл. 6.
Таблица 6
PВариант 7
У пятидесяти новорождённых измеряли массу тела с точностью до 10 г. Результаты измерений приведены в таблице 7.
Таблица 7
| 3,70 | 3,85 | 3,70 | 3,78 | 3,60 | 4,45 | 4,20 | 3,87 | 3,30 | 3,76 |
| 3,75 | 4,03 | 3,75 | 4,18 | 3,80 | 4,75 | 3,25 | 4,10 | 3,55 | 3,35 |
| 3,38 | 3,30 | 4,15 | 3,95 | 3,50 | 3,88 | 3,71 | 3,15 | 4,15 | 3,80 |
| 4,22 | 3,75 | 3,58 | 3,55 | 4,08 | 4,03 | 3,24 | 4,05 | 3,56 | 3,05 |
| 3,58 | 3,98 | 3,88 | 3,78 | 4,05 | 3,40 | 3,80 | 3,06 | 4,38 | 4,20 |
PВариант 8
Получены данные коэффициента интеллекта семидесяти взрослых людей. Результаты измерений приведены в таблице 8.
Таблица 8
PВариант 9
Психолог проводит групповой тренинг. Получены данные уровня тревожности у 80 участников тренинга. Результаты измерений приведены в таблице 9:
Таблица 9