Генеральная и выборочная совокупность

Математическая статистика

Первичная обработка данных

Главная цель расчёта – не цифры,

а понимание.

Генеральная и выборочная совокупность

ÆГенеральной совокупностью называется множество объектов произвольной природы, обладающих признаками, доступными для наблюдения и количественного измерения.

ÆОбъекты, входящие в генеральную совокупность, называются её элементами, а их общее число – её объёмом.

Предположим, из генеральной совокупности случайным образом извлекаем элементы, значения некоторого признака для них записываем как . Эти значения называются наблюдениями, их набор – выборкой. Количество наблюдений каждого из признаков обозначим и назовём частотами. Число наблюдений 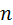называем объёмом выборки: .

ÆОсновная задача математической статистики – сделать научно обоснованные выводы о распределении одной или более неизвестных случайных величин или их взаимосвязи между собой.

ÆВыборочным методом называется метод решения этой задачи посредством анализа выборки, полученной в результате многократных наблюдений.

Для того чтобы характеристики случайной величины, полученные выборочным методом, были объективны, необходимо, чтобы выборка была репрезентативной, т. е. достаточно хорошо представляла исследуемую величину. В силу закона больших чисел можно утверждать, что выборка будет репрезентативной, если её осуществлять случайно, т. е. все объекты генеральной совокупности имеют одинаковую вероятность попасть в выборку [1] .

ÆВыборка называется повторной, если отобранный объект перед выбором следующего возвращается в генеральную совокупность. Выборка называется бесповторной, если отобранный объект в генеральную совокупность не возвращается. На практике обычно имеют дело с бесповторными выборками.

ÆВсякая случайная величина имеет определённую функцию распределения и другие числовые характеристики, которые называются теоретическими, в отличие от выборочных, которые определяются по наблюдениям.

ÆРяд наблюдений, упорядоченных по возрастанию, называется вариационным рядом. Его члены обозначаются и называются вариантами.

Наименьшее и наибольшее значения вариант обозначаются и 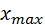, их называются крайними членами вариационного ряда. Число называется размахом выборки.

В случае наблюдений дискретной случайной величины одно и то же значение можно встретить несколько раз. Такие значения 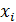случайной величины записывают с указанием 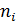- числа раз его появления в наблюдениях, это и есть частота данного значения.

Вариационный ряд в общем виде можно записать как

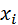
В случае непрерывной случайной величины на практике часто применяют группировку.

Отрезок наблюдаемых значений называют интервалом наблюдений.

Интервал наблюдений разбивают на частичных интервалов одинаковой длины .

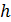ÆРекомендуемое число интервалов вычисляют по формуле Стерджеса [3] .

Длину частичных интервалов вычисляют как .

Затем подсчитывают числа попаданий наблюдений в эти интервалы, которые принимают за частоты . Малочисленные частоты, значения которых меньше 5 ( 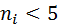), следует объединить, в этом случае надо объединить и соответствующие интервалы.

В качестве новых значений вариант 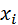берут середины интервалов .

Þ Примечание. Группировка связана с потерей части полезной информации, заключённой в выборке. Однако она имеет и свои преимущества. Оценим величину экономии, например, выполнено 1000 наблюдений некоторого признака. Рекомендуемое число интервалов: 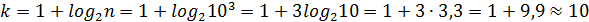. Отсюда видно, что требуется обработать числа вместо 1000.

Группировку можно применять и в случае дискретной случайной величины, если шаг, с которым меняются её значения, слишком мал.

ÆЧисло называется относительной частотой.

ÆНабор вариант 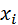(или частичных интервалов) и их относительных частот называется статистическим рядом.

Статистический ряд для дискретной случайной величины:

Варианта
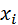
Частота
Относительная частота

Статистический ряд для непрерывной случайной величины:

Интервалы
Середина интервала
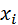
Частота
Относительная частота

 

Графически статистические ряды можно представить в виде полигона, гистограммы или графика накопленных частот.

ÆПолигон частот – это ломаная линия, отрезки которой соединяют точки , , …, .

ÆПолигон относительных частот – это ломаная линия, отрезки которой соединяют точки , , …, .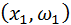

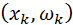Þ Примечание. Полигоны обычно служат для изображения выборки в случае дискретных случайных величин.

ÆНакопленные частоты будем обозначать , где . Очевидно, что эти величины получены суммированием частот, т. е. , что эти величины не убывают.

ÆНакопленные относительные частоты обозначим , где . Очевидно, что эти величины также не убывают.

 

?Упражнение 1. Постройте полигоны частот и относительных частот, найдите накопленные относительные частоты, запишите эмпирическую функцию распределения по данному вариационному ряду:

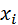
Решение

Найдём объём выборки и дополним таблицу относительными и накопленными относительными частотами.

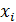
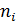
Варианты	Частота	Относительная частота	Накопленная относительная частота
		0,2	0,2
		0,3	0,5
		0,1	0,6
		0,4
Объём выборки:

 

 

 

 

Запишем эмпирическую функцию распределения, используя накопленные относительные частоты:

 

ÆГистограммой частот называется ступенчатая фигура, состоящая из прямоугольников, основанием которых служат частичные интервалы длиною 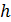, а высоты равны .

Величина называется плотностью частоты.

ÆГистограммой относительных частот называется ступенчатая фигура, состоящая из прямоугольников, основанием которых служат частичные интервалы длиною 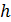, а высоты равны .

Величина называется плотностью относительной частоты.

Þ Примечание. Гистограмма обычно служит для изображения выборки в случае непрерывных случайных величин. Очевидно, площадь гистограммы относительных частот равна единице. Поэтому гистограмму относительных частот можно рассматривать как график эмпирической (выборочной) плотности распределения, в этом и заключается практическая польза гистограммы относительных частот.

ÆГрафиком накопленных частотназывается ступенчатая фигура, состоящая из прямоугольников, основанием которых служат частичные интервалы длиною 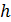, а высоты равны накопленным относительным частотам. Заметим, что график накопленных относительных частот имеет вид ступенчатой «лестницы» (от 0 до 1).

Þ Примечание. График накопленных относительных частот и эмпирическая функция распределения на практике используются для приближения теоретической функции распределения [3].

?Упражнение 2. Постройте гистограммы частот и относительных частот, график накопленных относительных частот, запишите эмпирическую функцию распределения по данному распределению выборки:

Частичный интервал	[2,7)	[7,12)	[12,17)	[17,22)	[22,27)
Число наблюдений, попавших в интервал,

Решение

Найдём объём выборки (50), длину интервала (5), построим таблицу, где вычислены относительные и накопленные относительные частоты, плотности частот и относительных частот, которые потребуются при построении соответствующих гистограмм.

 

Частичный интервал	Частота	Относительная частота	Накопленная относительная частота	Плотность частоты	Плотность относительной частоты
[2; 7)		0,1	0,1		0,02
[7; 12)		0,2	0,3		0,04
[12; 17)		0,5	0,8		0,1
[17; 22)		0,12	0,92	1,2	0,024
[22; 27)		0,08		0,8	0,016
Объём выборки: 50	Площадь гистограммы частот: 50
Длина интервала:

 

 

 

 

 

 

Используя накопленные относительные частоты, запишем эмпирическую функцию распределения: