Метод Квайна - Мак-Класки

Разберем его на примере. Рассмотрим функцию четырех переменных, заданную вектором своих значений

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

(0 0 0 1 1 1 1 1 0 0 1 1 1 0 0 0).

Сверху над каждым значением функции проставлен номер набора, на котором функция это значение принимает.

Теперь по номерам наборов, восстановим те из них, на которых функция равна 1.

Это наборы (0011), (0100), (0101), (0110), (0111), (1010), (1011), (1100).

Далее мы выполним действия, которое не нужны для построения минимальной ДНФ, но полезны с точки зрения лучшего усвоения материала. Выпишем конституенты 1, соответствующие каждому набору.

.

СДНФ такова

.

Конституенты и , например, можно склеить в импликанту, содержащую только три буквы, так как

.

Но гораздо удобнее склеивать не формулы, а двоичные наборы, соответствующие этим формулам. В самом деле, : одинаковые цифры остаются, а цифры 0 и 1 взаимно “уничтожают” друг друга. Ясно, что склеивать вместе можно только два набора одинаковой длины и только такие, которые различаются в одной позиции.

Рассортируем исходные 8 различных наборов длины 4 по числу единиц в них: нет единиц, одна единица,…, четыре единицы. Расположим наборы с одинаковым числом единиц в столбцы. Склейки возможны только между наборами из соседних столбцов. Соединим линиями наборы, которые можно склеить (рис.1).

Рис. 1

Выполним все 8 возможных склеек. Исчезнувшие цифры заменим черточкой. В результате склеек образуется 8 импликант - 010_; 01_0; _100; 0_11; _011; 01_1; 011_; 101_.

Ни одной конституенты, содержащей 4 буквы и соответствующей набору длины 4 не осталось. Каждая из получившихся импликант содержит 3 буквы и “поглотила” две конституенты.

Вновь рассортируем наборы по номеру места, на котором стоит черточка. Ясно, что склеивать вместе можно только те наборы, у которых совпадает положение черточки. Соединим линиями наборы, которые склеиваются (рис. 2).

Рис. 2

В итоге получилось 5 наборов - _100; _011; 0_11; 01_ _; 101_, которые далее нельзя склеить. Эти наборы соответствуют таким ипликантам единицы: .

Выпишем сокращенную ДНФ нашей функции

.

Продолжим процесс минимизации, для чего составим таблицу, которая называется таблицей Квайна(табл.1). В первой строке таблицы перечислим все восемь исходных наборов длины 4, соответствующих конституентам единицы данной функции . В первом столбце запишем 5 наборов, получившихся в результате всех возможных склеек. Эти наборы, как уже было сказано, соответствуют слагаемым сокращенной ДНФ функции . Во внутренних клетках таблицы поставим 1, если данная импликанта “содержит в себе” данную конституенту.

Таблица 1

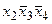
	_100	1					1
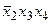
	_011		1
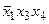
	0_11		1
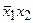
	01_ _			1+	1			1
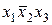
	101_					1			1

В соответствии с построением, для каждой конституенты имеется хотя бы одна импликанта, “поглотившая” ее. При этом четыре из пяти импликант “поглотили” по две конституенты, а импликанта 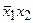- четыре. Значит, в каждом столбце таблицы стоит хотя бы одна единица; в каждой строке – не менее двух единиц.

Чтобы получить минимальную ДНФ, нужно выбрать из первого столбца таблицы импликанты, “содержащие в себе” все 8 конституент и обойтись при этом минимальным числом букв.

Начнем с определения ядра функции. Конституенту 1100 “поглотила” только импликанта _100; конституенту 1010 - только импликанта 101_; конституенты 0101 и 0110 “содержатся” только в импликанте 01_ _.

Ядро функции таково: . Три импликанты, составляющие ядро, “содержат в себе” 7 из 8 конституент. Не выбранной осталась конституента 0011, которая “содержится” в двух импликантах: _011 и 0_11. Чтобы получить минимальную ДНФ, нужно добавить к ядру любую из этих импликант. Следовательно, минимальных ДНФ две и можно записать

Минимальная КНФ по методу Квайна – Мак-Класки строится так же. Конституенты и импликанты нуля склеиваются в соответствии с равносильностью 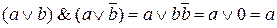. Например,

или (011)&(010)→(01_).

Построим минимальную КНФ нашей функции. Сначала выпишем наборы, на которых функция равна 0. Одновременно покажем, какие конституенты нуля соответствуют каждому набору (табл .2).

Таблица 2

Набор	Конституента нуля	Набор	Конституента нуля

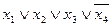
Осуществим склейки (рис. 3).

1101 0001

1111 1001 0010 0000

1110 1000

Рис. 3

В результате имеем 8 импликант нуля, ни одной конституенты нуля не осталось. Продолжим склеивание (рис. 4)

_001 1_01 11_1 100_

_000 00_0 111_

000_

Рис. 4

Получились 5 различных импликант нуля - _00_; 1_01; 11_1; 00_0; 111_. Дальнейшие склейки невозможны.

Составим таблицу Квайна (табл.3). В ее клетках поставим нули, если данная импликанта нуля “содержит в себе” данную конституенту нуля. В соответствии с построением, в каждом столбце таблицы строит хотя бы один 0, а в каждой строке – два (четыре) нуля.

Таблица 3

	_00_	0	0		0	0
	1_01						0
	11_1						0
	00_0			0
	111_							0	0

Ядро функции – множество импликант . Только конституента “не содержится” в импликантах ядра. Ее “содержат” две импликанты , , минимальных КНФ две,

.