Основные определения
ЛЕКЦИЯ 2.4.
Минимизация логических функций
Краткое содержание лекции
· Конституенты нуля и единицы; импликанты нуля и единицы; сокращенные, тупиковые, минимальные КНФ и ДНФ данной функции
· Метод Квайна – Мак-Класки построения минимальной ДНФ и КНФ данной функции
· Минимизация функций при помощи карт Карно
· Минимизация не полностью определенных функций
Основные определения
Определение. Всякая правильная полная относительно переменных  элементарная конъюнкция
элементарная конъюнкция  (элементарная дизъюнкция
(элементарная дизъюнкция 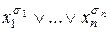 ) называется конституентой единицы (конституентойнуля). Всякая конституента единицы (конституента нуля) равна 1 (0) наединственном наборе значений переменных -
) называется конституентой единицы (конституентойнуля). Всякая конституента единицы (конституента нуля) равна 1 (0) наединственном наборе значений переменных - 

соответственно).
Определение. Правильная, но не полная ЭК (ЭД) называется импликантой единицы (импликантой нуля). Например, если имеются четыре переменных -  , то импликантами единицы будут такие ПЭК:
, то импликантами единицы будут такие ПЭК:  . Импликанты нуля – это, например, следующие ПЭД:
. Импликанты нуля – это, например, следующие ПЭД: 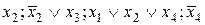 . Если задана импликанта 1 (импликанта 0)
. Если задана импликанта 1 (импликанта 0) 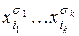 (
(  ), то она равна 1 (равна 0) уже на
), то она равна 1 (равна 0) уже на  наборах.
наборах.
Именно, значения переменных, входящих в импликанту, определяются однозначно,  (
(  ), значения остальных n-k переменных могут быть любыми, всего
), значения остальных n-k переменных могут быть любыми, всего  вариантов.
вариантов.
Скажем, что всякая импликанта единицы (импликанта нуля) “содержит в себе”(«включает в себя», «поглотила»)  конституент единицы (конституент нуля).
конституент единицы (конституент нуля).
Например, импликанта единицы  “содержит в себе”
“содержит в себе”  конституенты единицы -
конституенты единицы -  .
.
Импликанта нуля  “включает в себя” две конституенты нуля -
“включает в себя” две конституенты нуля -  .
.
Определение. Конституента единицы 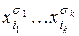 (конституента нуля
(конституента нуля 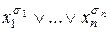 ) называется конституентой единицы функции
) называется конституентой единицы функции  (конституентой нуля функции
(конституентой нуля функции  ), если
), если  (
(  ).
).
Следовательно, СДНФ функции  - это дизъюнкция всех конституент единицы функции
- это дизъюнкция всех конституент единицы функции  . СКНФ функции
. СКНФ функции  - это конъюнкция всех ее конституент нуля.
- это конъюнкция всех ее конституент нуля.
Определение. Импликанта единицы  (импликанта нуля
(импликанта нуля  ) называется импликантой единицы функции
) называется импликантой единицы функции  (импликантой нуля функции
(импликантой нуля функции  ), если
), если  на всехнаборах значений переменных, на которых равна 1 импликанта
на всехнаборах значений переменных, на которых равна 1 импликанта 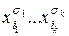 (
(  на всех наборах значений переменных накоторых равна 0 импликанта
на всех наборах значений переменных накоторых равна 0 импликанта 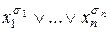 ).
).
«Две конституенты единицы (импликанты единицы) можно “склеить” в импликанту единицы с меньшим числом букв, вследствие равносильности 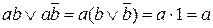 .
.
Например,  .
.
Две конституенты нуля (импликанты нуля) можно “склеить” в импликанту нуля с меньшим числом букв, вследствие равносильности  . Например,
. Например,  ».
».
Рассмотрим множество всех импликант единицы (импликант нуля) данной функции  , которое получается в результате проведения всех возможных склеек исходных конституент единицы (конституент нуля) функции
, которое получается в результате проведения всех возможных склеек исходных конституент единицы (конституент нуля) функции  .
.
Определение. Дизъюнкция всех импликант единицы (конъюнкция всех импликант нуля) множества импликант единицы (импликант нуля) называется сокращенной ДНФ (сокращенной КНФ) данной функции  .
.
Сокращенная ДНФ (сокращенная КНФ) равносильна функции  , так как у них совпадают таблицы истинности. Сокращенная ДНФ и функция
, так как у них совпадают таблицы истинности. Сокращенная ДНФ и функция  по построению принимают значение 1 на одних и тех же наборах значений переменных; сокращенная КНФ и функция
по построению принимают значение 1 на одних и тех же наборах значений переменных; сокращенная КНФ и функция  по построению принимают значение 0 на одних и тех же наборах значений переменных.
по построению принимают значение 0 на одних и тех же наборах значений переменных.
Сокращенная ДНФ (сокращенная КНФ) может содержать "лишние" импликанты, удаление которых не меняет таблицы истинности этой сокращенной ДНФ (сокращенной КНФ). Если у сокращенной ДНФ (сокращенной КНФ) удалить "лишние" импликанты, получается ДНФ (КНФ), которая называется тупиковой.
Представление функции тупиковой ДНФ (тупиковой КНФ) в общем случае не единственно.
Определение. Ядромфункции  называется множество импликант единицы (импликант нуля), входящих во все тупиковые ДНФ (КНФ)функции
называется множество импликант единицы (импликант нуля), входящих во все тупиковые ДНФ (КНФ)функции  . (К сожалению, здесь имеет место совпадение терминов).
. (К сожалению, здесь имеет место совпадение терминов).
Тупиковая ДНФ (КНФ) с наименьшим числом букв называется минимальной ДНФ (минимальной КНФ) функции  .Минимальных ДНФ (КНФ) может быть несколько, но все они содержат одинаковое число букв.
.Минимальных ДНФ (КНФ) может быть несколько, но все они содержат одинаковое число букв.
Разберем два метода построения минимальной ДНФ. Используя принцип двойственности, можно легко перенести эти методы на случай построения минимальной КНФ.