Вероятностные свойства серии измерений

Лекция № 5. Методы обработки результатов измерений.

 

Учет и исключение (или уменьшение) систематической погрешности представляют одну из самых сложных задач теории измерений. Способы решения этой задачи зависят от конкретных видов измерений, и не существует общей методики ее решения. Часто используется подход, основанный на всестороннем теоретическом анализе процедуры измерения и характеристик применяемой аппаратуры. Такой анализ может дать оценку границ систематической погрешности. При точных измерениях оценка систематической погрешности производится по результатам измерения искомой величины различными, принципиально независимыми методами с применением различной аппаратуры. Многие современные способы анализа систематической погрешности используют аппарат математической статистики (дисперсионный, регрессионный, корреляционный, спектральный анализ), теории принятия решений, теории игр и др.

Случайная погрешность в большинстве случаев может быть уменьшена с помощью относительно простой статистической обработки результатов измерений.

Промахи относятся к аномальным результатам измерений, которые могут быть следствием кратковременного воздействия на процесс измерения некоторого мешающего фактора, преобладающего над остальными. Промах может быть вызван ошибкой оператора, проводящего измерение, или сбоем измерительной аппаратуры. В этих случаях аномальный результат должен быть отброшен. Однако отбрасывание аномальных данных является спорным вопросом, по которому у специалистов нет единого мнения. Например, из истории физики известно, что именно аномальные результаты экспериментов привели к великим открытиям. Поэтому при научных исследованиях и в большинстве технических измерений необходимо тщательно проанализировать причину промаха, в частности, многократно повторив эксперимент. Тем не менее, в хорошо изученной ситуации, если не удается найти внешнюю причину промаха, вопрос об отбрасывании аномального отсчета должен быть решен на основе обработки всех данных эксперимента.

Пусть имеется N наблюдений одной и той же величины, в результате которых получены отсчеты x₁, x₂,…,x­_N. Интересующее нас событие произошло, если отсчет .

Тогда вероятностью события называется предел, к которому стремится отношение числа m наступления этого события к числу N всех измерений при числе измерений стремящемся к бесконечности

.

Распределением вероятности F(x) называется вероятность того, что значение x некой случайной величины лежит в пределах

.

Пользуясь понятием распределения вероятностей можно найти вероятность того, что событие принадлежит некому интервалу

.

Вероятность принадлежности значения бесконечно малому интервалу можно выразить как

,

где - плотность вероятности.

Для плотности вероятности верно

.

Гистограмма распределения показывает, как часто встречаются те или иные отсчеты.

Рис. 5

По оси x откладывают границы интервалов, по оси y – относительную частоту попадания отсчетов в интервал

.

При и гистограмма превращается в график плотности вероятности.

Математическое ожидание m - число в окрестности которого концентрируются значения случайной величины:

.

Дисперсия D – это число, которое характеризует степень рассеяния значений случайной величины вокруг её математического ожидания

.

Величина называется средним квадратическим отклонением.

Нормальным распределением случайной величины называется распределение плотность которого равна

.

Важнейшие свойства нормального распределения

1. Если x имеет нормальное распределение 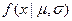, то и имеет нормальное распределение .

2. Если x₁ и x₂ имеют нормальные распределения и , то имеют нормальное распределение .